A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
CURRENT ELECTRICITY
CP SINGH|Exercise Exercise|137 VideosView PlaylistCAPACITANCE
CP SINGH|Exercise Exercise|74 VideosView PlaylistELECTROMAGNETIC INDUCTION
CP SINGH|Exercise EXERCISES|141 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
CP SINGH-CURRENT ELECTRICITY-Exercise
- . (i) i= 2 A (ii) i1 = (10)/(3) A (iii) i2 = - (4)/(3) A.
05:20
|
Play - In the circuit, the galvanometer G shows zero deflection. If the batte...
02:59
|
Play - In the given circuit currents I1 and I2 are .
02:22
|
Playing Now - The potential difference between A and B is .
02:39
|
Play - In the given circuit (Choose the incorrect option).
05:39
|
Play - When some potential differece is maintained between A and B, current I...
08:54
|
Play - Two cells of unequal emfs epsilon1 and epsilon2, and internal resistan...
03:45
|
Play - An accumulator battery (storage cell) B of emf epsilon and internal re...
01:58
|
Play - In the circuit shown in the figure, if potentail at point A is taken t...
02:19
|
Play - See the electrical circuit shown in this figure. Which of the followin...
01:48
|
Play - Two resistance R(1) and R(2) are joined as shown in figure to two batt...
03:07
|
Play - Find out the value of current through 2Omega resistance for the given ...
02:35
|
Play - A battery is charged at a potential of 15 V for 8 hours when the curre...
02:37
|
Play - The resistance of the coil of an emmeter is R. The shunt required to i...
02:33
|
Play - A milliammeter of range of 10 mA gives full-scale deflection for a cur...
02:37
|
Play - To use the milliammeter of the previous question as a voltmeter of ran...
02:57
|
Play - A voltmeter has a resistance G and range V. Calculate the resistance t...
03:37
|
Play - A galvanometer with 50 divisions on the scale has a resistance of 25 O...
02:50
|
Play - The net resistance of an ammeter should be small to ensure that
01:38
|
Play - The net resistance of a volmeter should be large to ensure that
01:59
|
Play
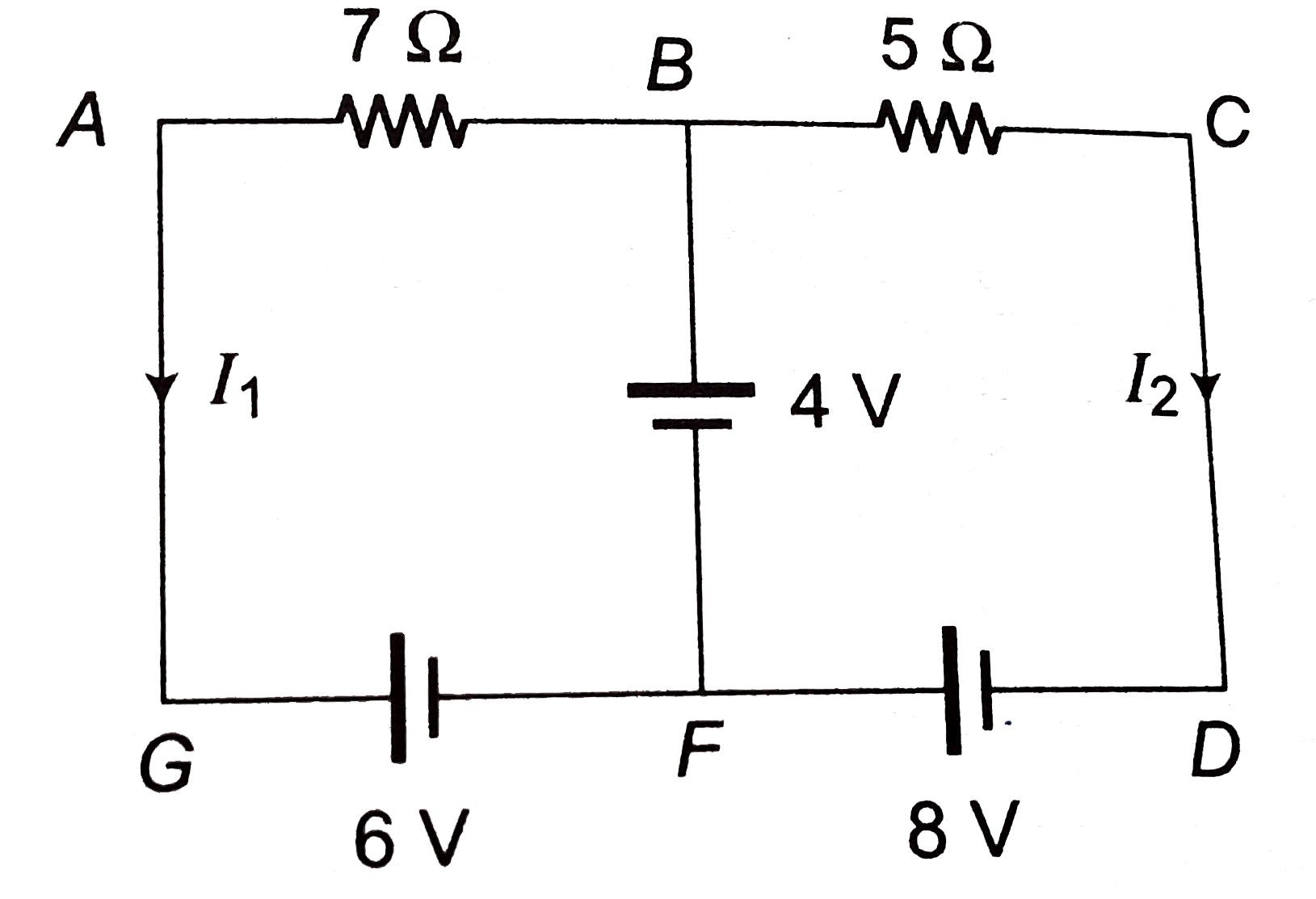 .
.