Text Solution
Verified by Experts
|
Topper's Solved these Questions
CENTER OF MASS
CP SINGH|Exercise Exercises|150 VideosView PlaylistCIRCULAR MOTION
CP SINGH|Exercise Exercise|90 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
CP SINGH-CENTER OF MASS-Exercises
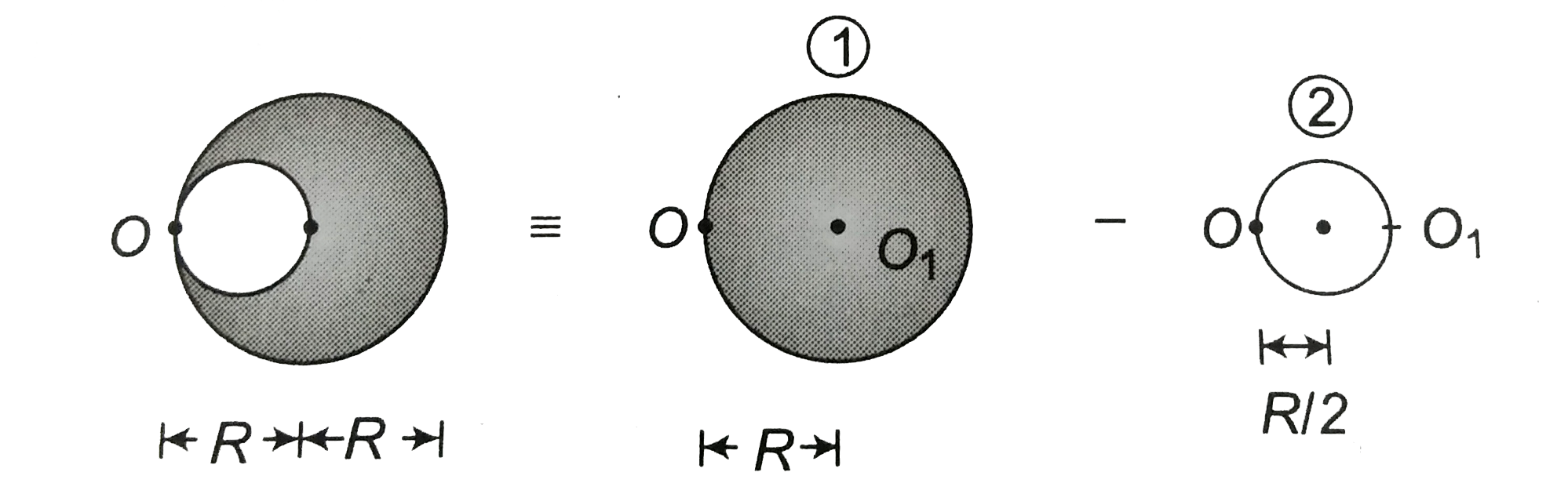
- From a circular disc of radius R, another disc of diameter R is remove...
04:53
|
Playing Now - Two blocks of mass 1kg and 3 kg have position v ectors hat(i) + 2 hat...
01:49
|
Play - All the particles of a body situated at distance d from the origin. Th...
01:18
|
Play - Particle of masses m, 2m,3m,…,nm grams are placed on the same line at ...
02:58
|
Play - Three identical metal balls each of radius r are placed touching each ...
01:22
|
Play - Look at the drawing given in the figure which has been drawn with ink ...
02:06
|
Play - A circular disc of radius R is removed from a bigger circular disc of ...
04:22
|
Play - A hemisphere and a solid cone have a common base. The center of mass o...
03:43
|
Play - If the linear density (mass per unit length) of a rod of length 3 m is...
03:34
|
Play - The mass per unit length of a non - uniform rod of length L is given m...
02:33
|
Play - A thin rod of length 'L' is lying along the x-axis with its ends at x...
03:09
|
Play - Which of the following is true for center of mass ? (i) The center o...
Text Solution
|
Play - A cubical block of ice of maas m and edge L is placed in a large tray ...
05:47
|
Play - Two paricle A and B initially at rest, move towards each other under m...
01:05
|
Play - A ladder is leaned against a smooth wall and it is allowed to slip on ...
04:35
|
Play - A pulley fixed to the ceiling carries a string with blocks of mass m a...
03:35
|
Play - Two balls are thrown simultaneously from top of tower in air as shown ...
04:35
|
Play - Which of the following statements are true ? (i) A uniform wooden pl...
Text Solution
|
Play - Which of the following statements is true ? (i) A car of mass M is t...
Text Solution
|
Play - A boy of mass 40 kg stands on a rail road car of mass 60 kg, moving wi...
03:08
|
Play - A boy (mass of 40 kg) is standing at one end of a boat (mass of 60 kg)...
04:03
|
Play