A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
|
Topper's Solved these Questions
CENTER OF MASS
CP SINGH|Exercise Exercises|150 VideosView PlaylistCIRCULAR MOTION
CP SINGH|Exercise Exercise|90 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
CP SINGH-CENTER OF MASS-Exercises
- A 2 kg ball , moving at 10 m//s , collides head - on with a 3 kg ball ...
04:49
|
Play - A ball of mass m moving at speed v makes a head on collision with an ...
02:57
|
Play - A ball is dropped from a height h onto a floor and rebounds to a heigh...
04:40
|
Playing Now - A body falling from a height of 10 m rebounds from the hard floor . It
04:48
|
Play - A ball is dropped from a height of 20 m on a floor for which e = 1//2....
02:07
|
Play - In the previous problem , time taken by the ball up to the third colli...
05:11
|
Play - A partical falls from a height h upon a fixed horizontal plane and re...
02:42
|
Play - A ball hits the floor and rebounds after an inelastic collision. In th...
03:59
|
Play - A ball of mass m moving with speed v(0) strikes a block of mass 3 m ke...
03:45
|
Play - In the previous problem , mass of the ball is 10 g and it is moving wi...
06:25
|
Play - Two blocks of masses 1 kg and 3 kg are moving with velocities 2 m//s a...
06:08
|
Play - Initially spring is in its natural length . The block of mass 3 kg in ...
04:03
|
Play - In the previous problem , the maximum elongation of the spring is
07:06
|
Play - When the spring is compressed to maximum , what fraction of incidetn t...
06:16
|
Play - If blocks collide elastically head - on , the ratio of maximum compres...
06:40
|
Play - Two identical blocks A and B , each of mass m resting on smooth floor ...
04:08
|
Play - The ball sticks to block C, then block Ccollides elastically , head - ...
08:43
|
Play - A particle of mass m moving with kinetic energy K, makes a head - on e...
04:22
|
Play - Two trolleys of mass m and 3 m are attached by a spring. The spring wa...
04:41
|
Play - A ball of mass 0.5 kg moving with a velocity of 2 m//s strikes a wall ...
02:42
|
Play
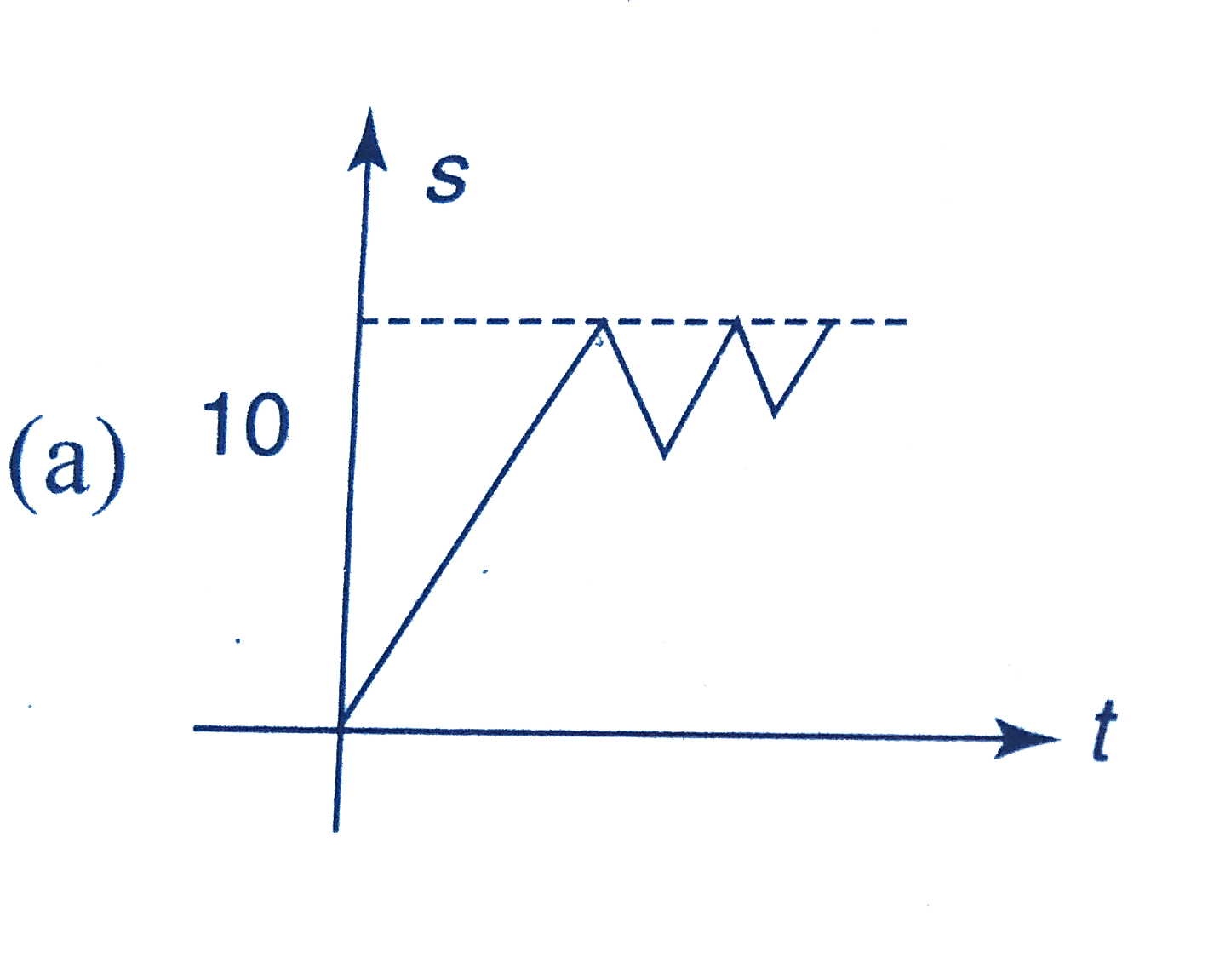 .
.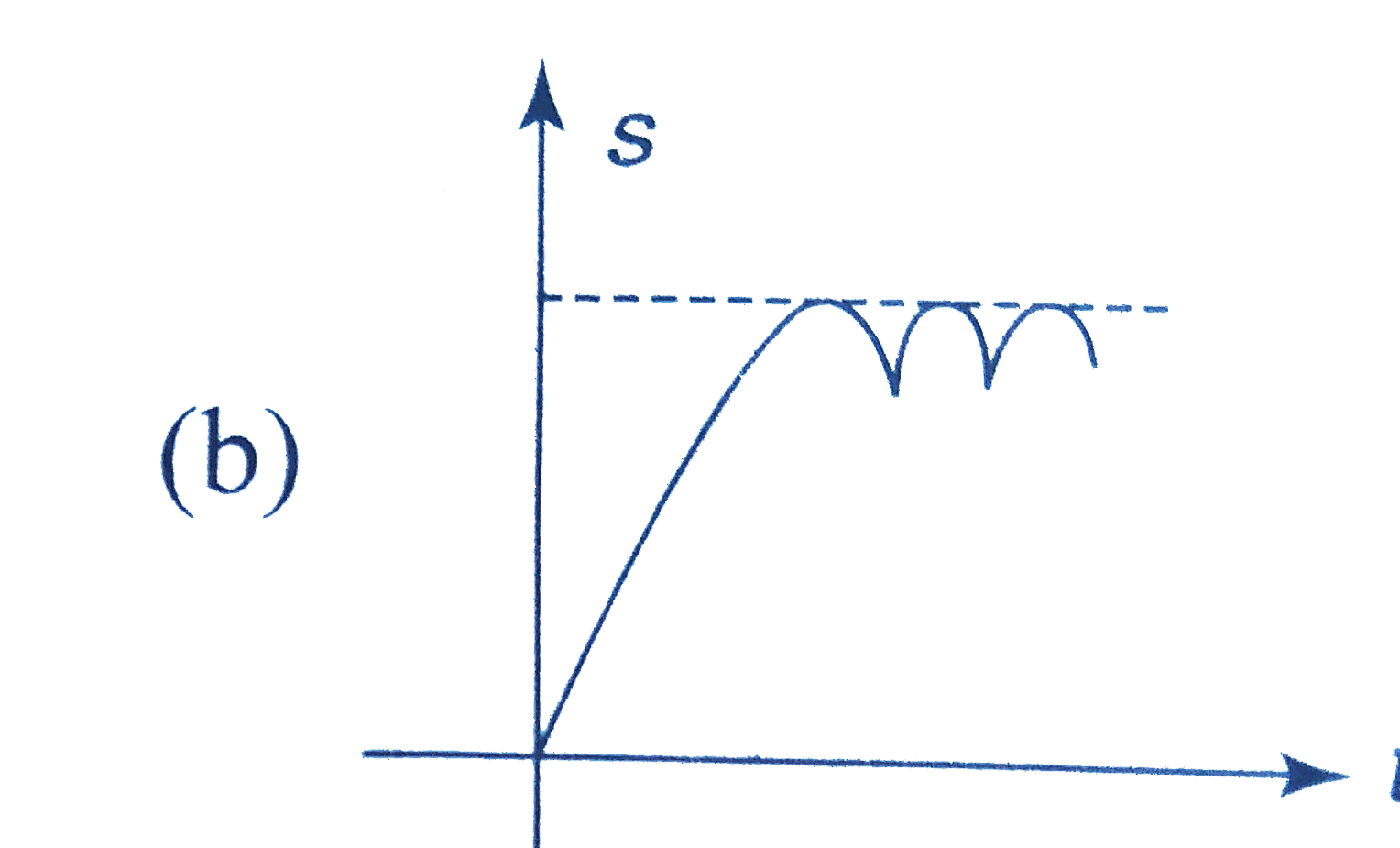 .
.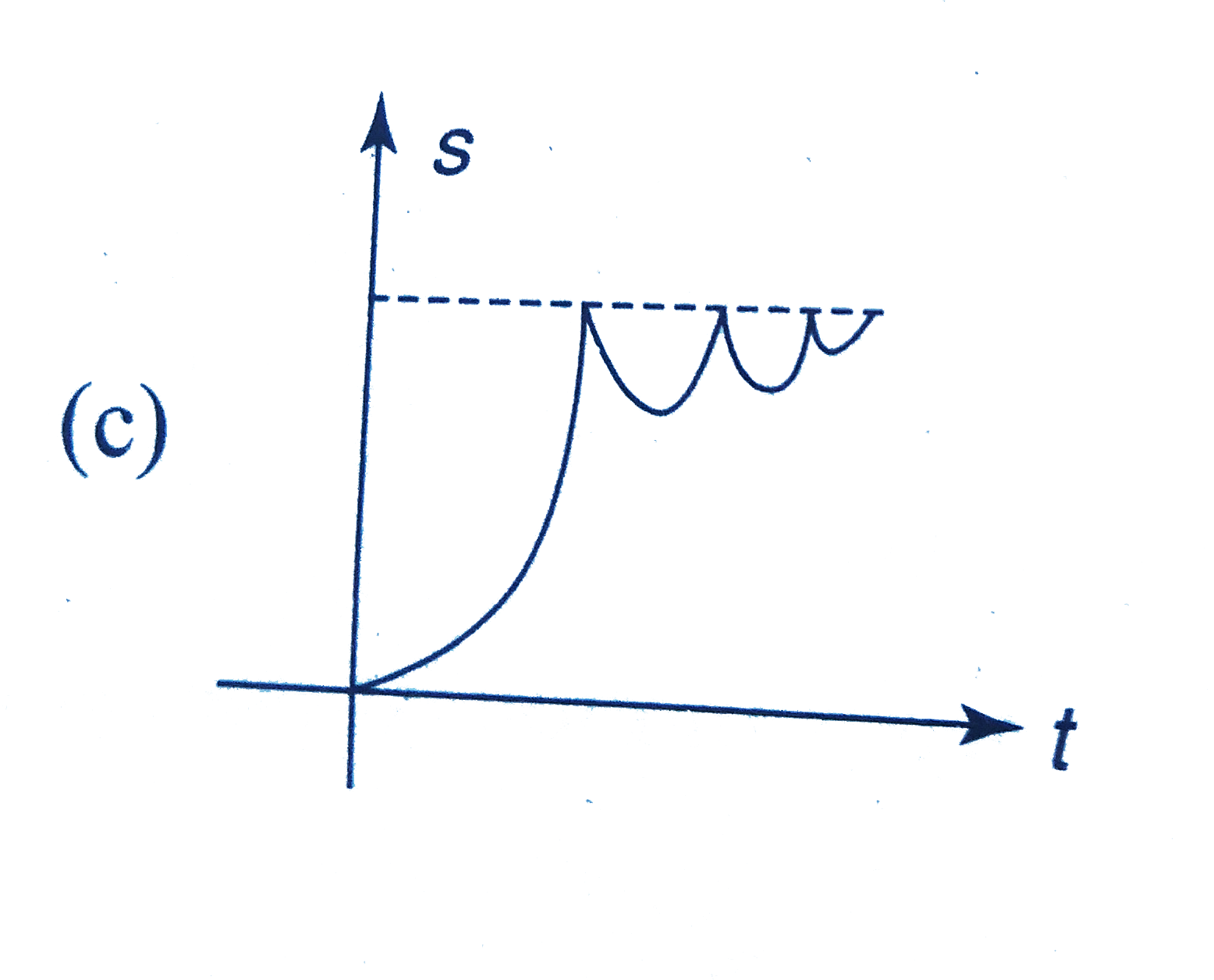 .
. .
.