A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
CENTER OF MASS
CP SINGH|Exercise Exercises|150 VideosView PlaylistCIRCULAR MOTION
CP SINGH|Exercise Exercise|90 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
CP SINGH-CENTER OF MASS-Exercises
- n balls each of mass m impinge elastically each second on a surface wi...
01:47
|
Play - A disc of mass 10 g is kept floating horizontally by throwing 10"marbl...
04:54
|
Play - If two balls each of mass 0.06 kg moving in opposite directions with s...
03:59
|
Play - In the figure given below, the position-time graph of a particle of ma...
03:20
|
Play - A force - time graph for a linear motion is shown in the figure where ...
03:57
|
Play - A bullet is fired from a gun. The force on the bullet is given by F=60...
05:46
|
Play - A particle of mass 2kg is initially at rest. A force starts acting on ...
03:23
|
Play - A particle of mass m , initially at rest , is acted upon by a variable...
02:39
|
Play - Two particles of masses m(1) and m(2) in projectile motion have veloci...
03:57
|
Play - Consider a rubber ball freely falling from a height h = 4.9 m onto a ...
04:11
|
Play - Two balls , having linear momenta vec(p)(1) = p hat(i) and vec(p)(2) =...
06:52
|
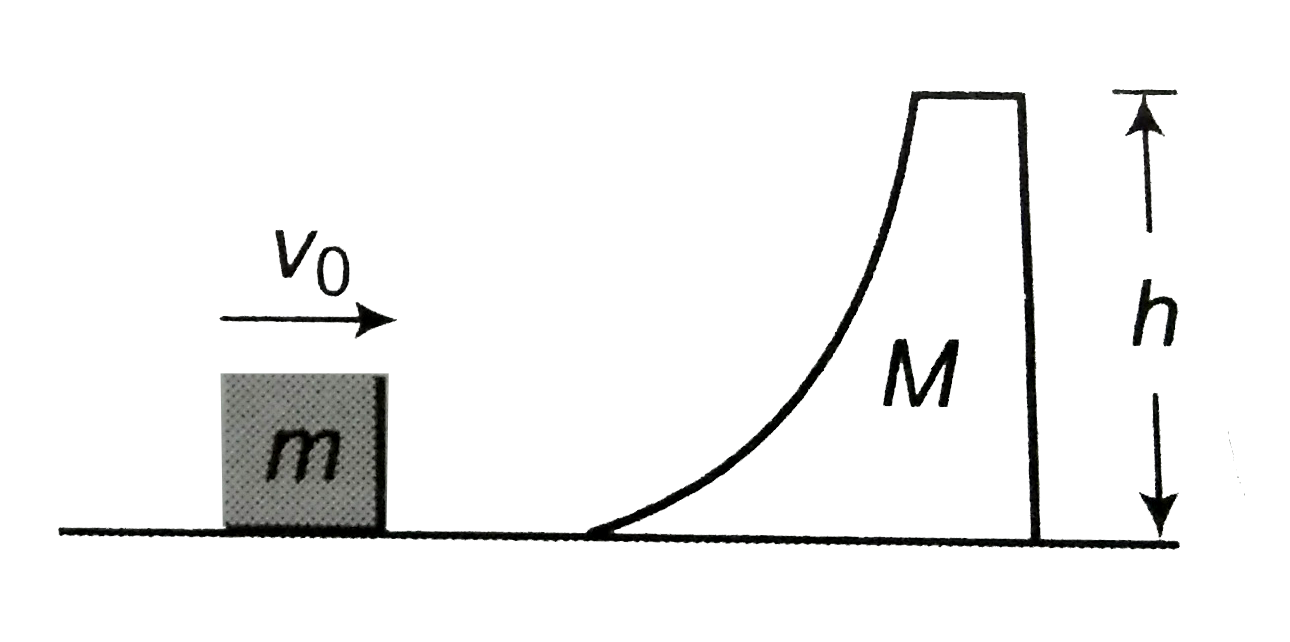
Play - A block of mass m is pushed towards the movable wedge of mass M and he...
04:03
|
Playing Now - Rocket works on the principle of coservation of
01:24
|
Play - Rocket propulsion is associated with
Text Solution
|
Play - The rate of mass of the gas emitted from the rear of a rocket is initi...
02:04
|
Play - A 500kg rocket is set for verticle firing. The exhaust speed is 800ms^...
02:50
|
Play - A satellite in a force - free space sweeps stationary interplanetary d...
01:57
|
Play - An explosion breaks a rock into three parts in a horizontal plane. Two...
Text Solution
|
Play - The force F acting on a partical of mass m is indicated by the force-t...
04:04
|
Play - A particle of mass 4 m which is at rest explodes into three fragments....
04:47
|
Play