Home
Class 9
MATHS
In the following figure, ABCD is a paral...

In the following figure, ABCD is a parallelogram and EFCD is a rectangle. Also, AL⊥DC. Prove that
(i) ar(ABCD)=ar(EFCD)
(ii) ar(ABCD)=DC×AL.

Answer

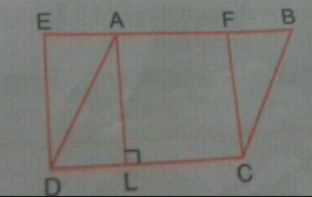
Step by step text solution for In the following figure, ABCD is a parallelogram and EFCD is a rectangle. Also, AL⊥DC. Prove that (i) ar(ABCD)=ar(EFCD) (ii) ar(ABCD)=DC×AL. by MATHS experts to help you in doubts & scoring excellent marks in Class 9 exams.

Doubtnut Promotions Banner Mobile Dark
|

Topper's Solved these Questions

  • ALGEBRAIC IDENTITIES

    RD SHARMA|Exercise All Questions|247 Videos

  • CIRCLE

    RD SHARMA|Exercise All Questions|306 Videos

Similar Questions

Explore conceptually related problems

In Fig. 9.13, ABCD is a parallelogram and EFCD is a rectangle.Also, A L_|_D C . Prove that (i) a r" "(A B C D)" "=" "a r" "(E F C D) (ii) a r" "(A B C D)" "=" "D C" "xx" "A L

In the adjoining figure, prove that ABCD is a parallelogram. Also find its area.

Knowledge Check

  • In the given figure, ABCD and AEFD a re two parallelograms. ar( Delta PEA) =

    A
    ar(`||^(gm) Delta`PEA)
    B
    ar(`Delta`PFD)
    C
    ar(`Delta`QFD)
    D
    ar(`||^(gm) Delta`CQPB)

  • In figure, if parallelogram ABCD and rectangle ABEM are of equal area, then

    A
    perimeter of ABCD = perimeter of ABEM
    B
    perimeter of `ABCD lt` perimeter of ABEM
    C
    perimeter of `ABCD gt` perimeter of ABEM
    D
    perimeter of `ABCD = (1)/(2)` (perimeter of ABEM)

    • Similar Questions

    Explore conceptually related problems

    In the adjoining figure, ABCD is a parallelogram and P is any points on BC. Prove that ar(triangleABP)+ar(triangleDPC)=ar(trianglePDA) .

    In the adjoining figure, MNPQ and ABPQ are parallelogram and T is any point on the side BP. Prove that (i) ar(MNPQ)=ar(ABPQ) (ii) ar(triangleATQ)=(1)/(2)ar(MNPQ) .

    In the following figure ABCD is a trapezium in which AB|| DC . Find the measdure of /_C .

    ABCD is a parallelogram. X and Y are mid-points of BC and CD. Prove that ar(triangleAXY)=3/8ar(||^[gm] ABCD)

    In the adjoining figure, ABCD is a parallelogram. Points P and Q on BC trisect BC. Prove that ar(triangleAPQ)=ar(triangleDPQ)=(1)/(6)ar(triangleABCD) .

    In the given figure, ABCD is a parallelogram. E and F are any two points on AB and BC, respectively. Prove that ar (triangleADF)=ar(triangleDCE) .

    Home
    Profile