Text Solution
Verified by Experts
|
Topper's Solved these Questions
NEWTONS LAWS OF MOTION
CP SINGH|Exercise EXERCISES|84 VideosView PlaylistNEET PREVIOUS YEAR
CP SINGH|Exercise Solved Questions|64 VideosView PlaylistRELATIVE MOTION
CP SINGH|Exercise EXERCISE|33 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
CP SINGH-NEWTONS LAWS OF MOTION-EXERCISES
- Two particles each of mass m are connected by a light string of length...
02:40
|
Playing Now - Action and reaction (i) act on two different objects (ii) have equ...
01:02
|
Play - A body of 5kg is moving with a velocity of 20m/s. If a force of 100N i...
00:58
|
Play - A car moving with a velocity of 10m/s can be stopped by the applicatio...
01:40
|
Play - A ball of mass 0.2 kg is thrown vertically upwards by applying a force...
03:42
|
Play - A force vector applied on a mass is represented as vec(F)=6hat(i)-8hat...
01:06
|
Play - A body of mass 2kg moving on a horizontal surface with an initial velo...
04:07
|
Play - A body of mass 1 kg is moving towards east with a uniform speed of 2m...
04:10
|
Play - A force F1 acts on a particle so as to accelerate it from rest to a ve...
02:41
|
Play - which of the following is correct order fo forces?
01:12
|
Play - A solid sphere of mass 2 kg is resting inside a cube as shown in fig. ...
03:23
|
Play - A particle of mass m is at rest at the origin at time t=0 It is subjec...
03:17
|
Play - Two bodies of mass 3kg and 4kg are suspended at the ends of massless s...
01:16
|
Play - Two masses m(1) and m(2) are connected by a light string passing over ...
02:30
|
Play - In fig the blocks A,B,and C of mass m each have acceleration a(1),a(2)...
04:09
|
Play - Three equal weight A,B and C of mass 2kg each are hanging on a string ...
02:11
|
Play - Two blocks are connected by a string as shown in the diagram. The uppe...
01:50
|
Play - Four identical blocks each of mass m are linked by threads as shown. I...
01:23
|
Play - A block of mass m(1) rests on a horizontal table. A string tied to the...
01:19
|
Play - A uniform chain of mass 2 kg hangs from a light pulley with unequal le...
05:36
|
Play - A string of negligible mass going over a clamped pulley of mass m supp...
03:33
|
Play
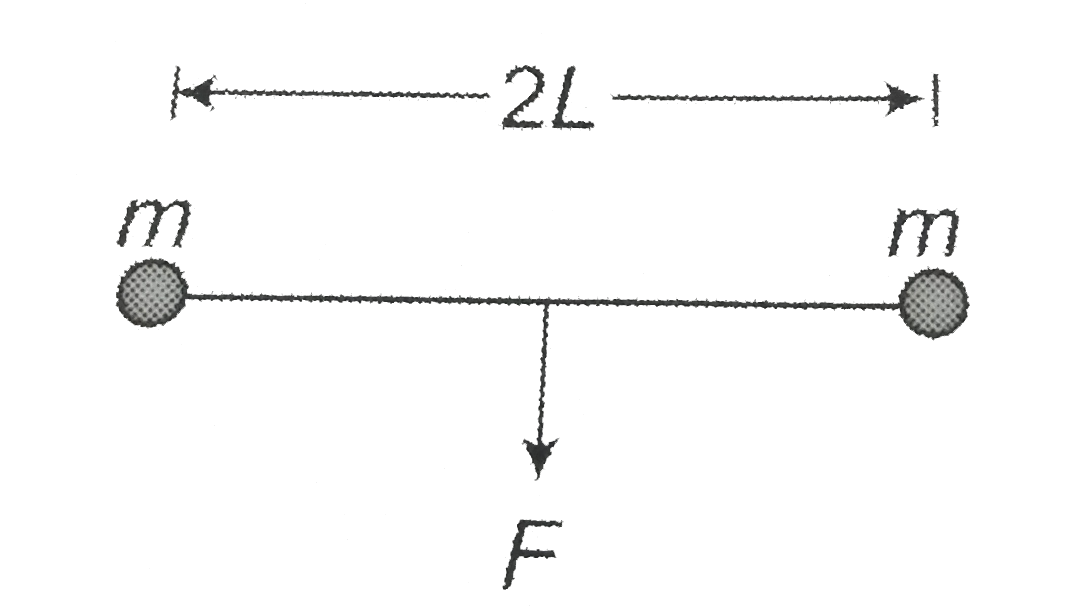
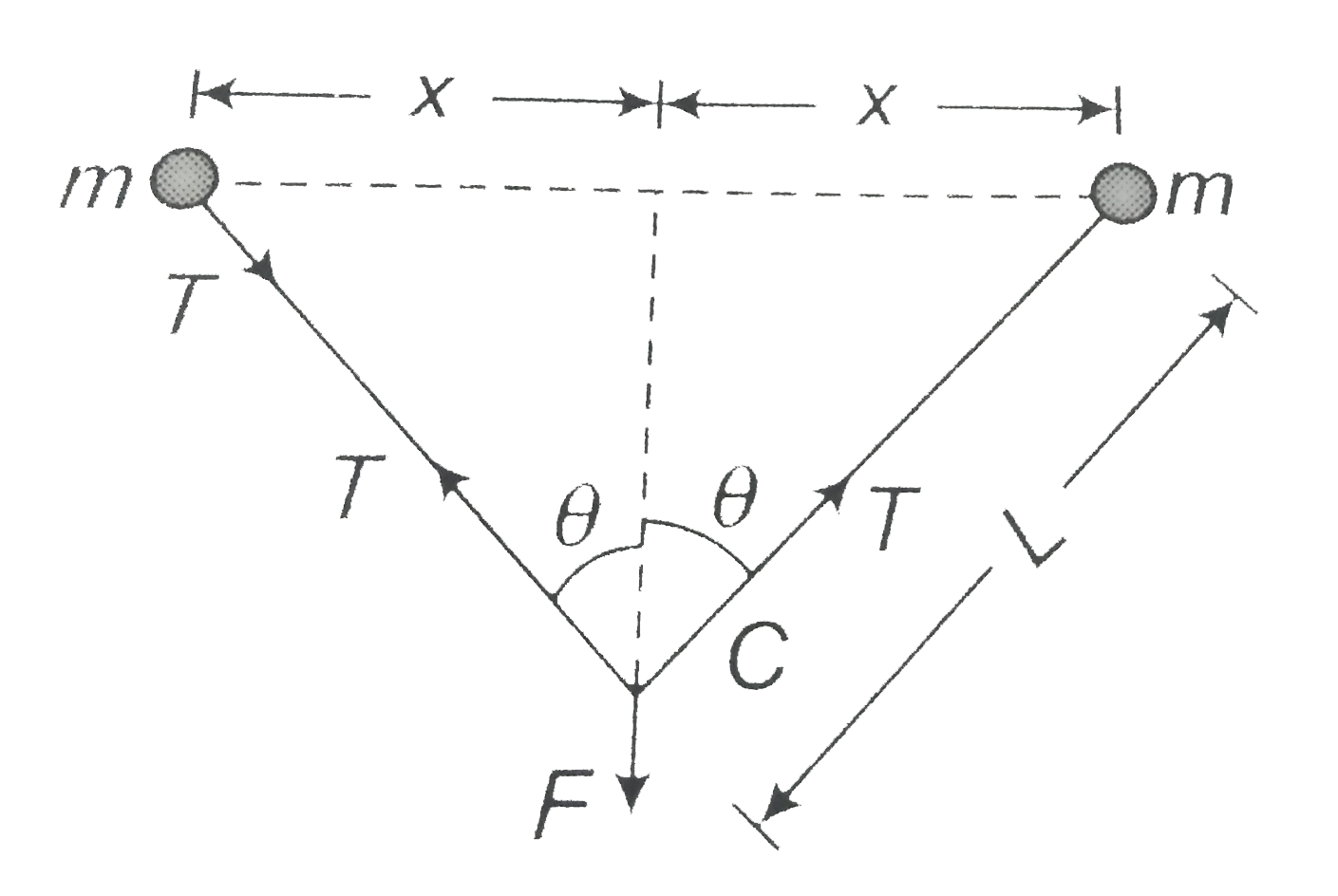 Point `C:`
Point `C:` 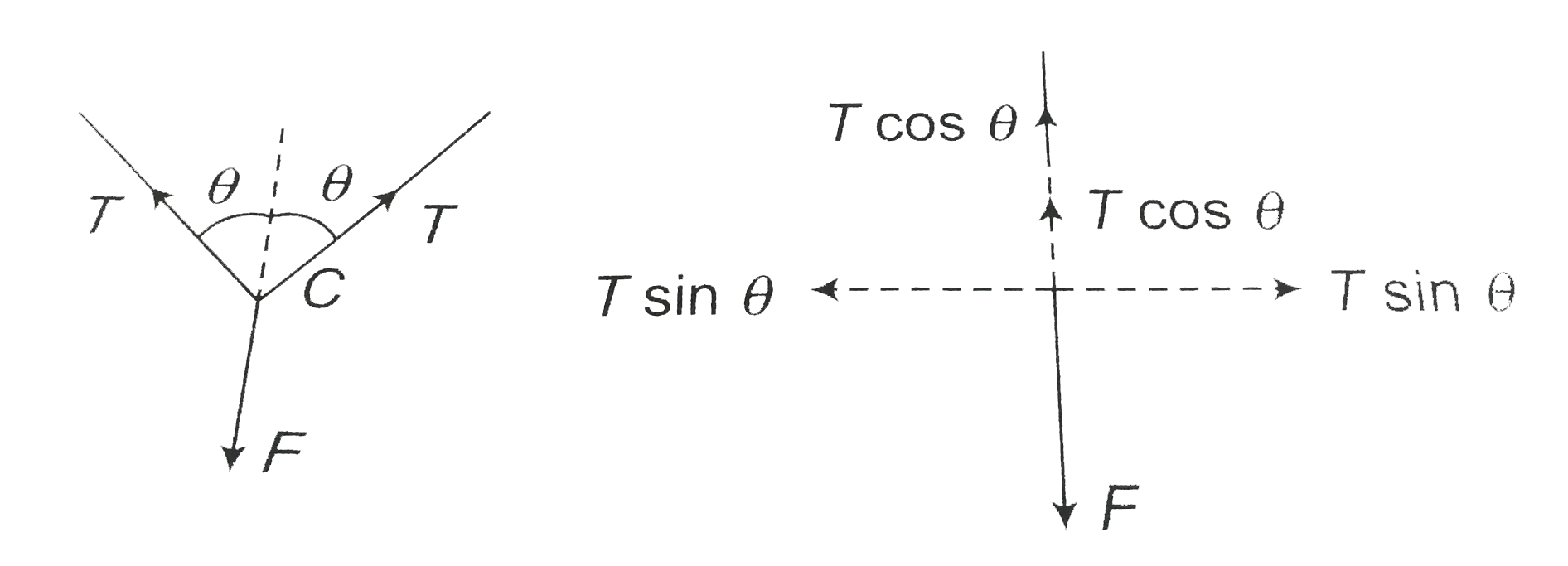
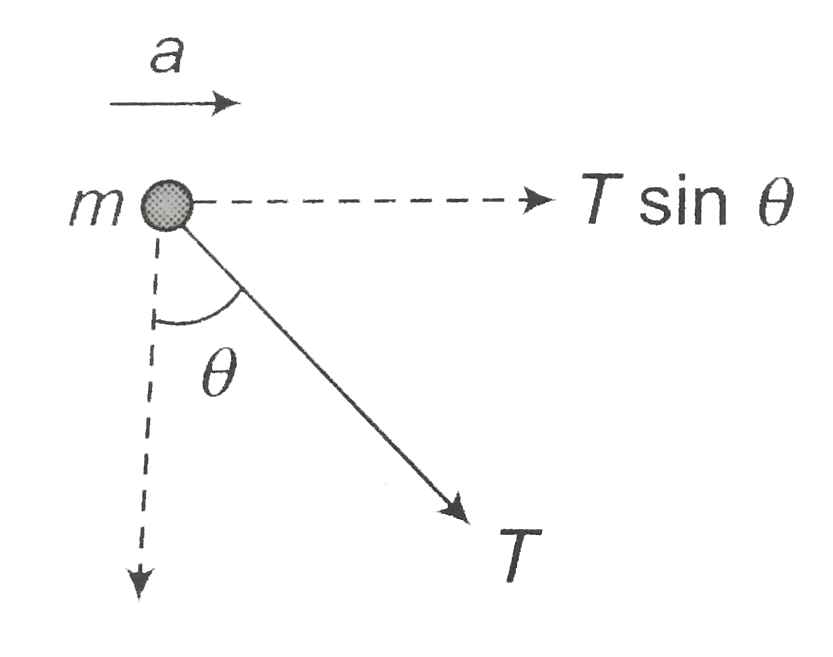
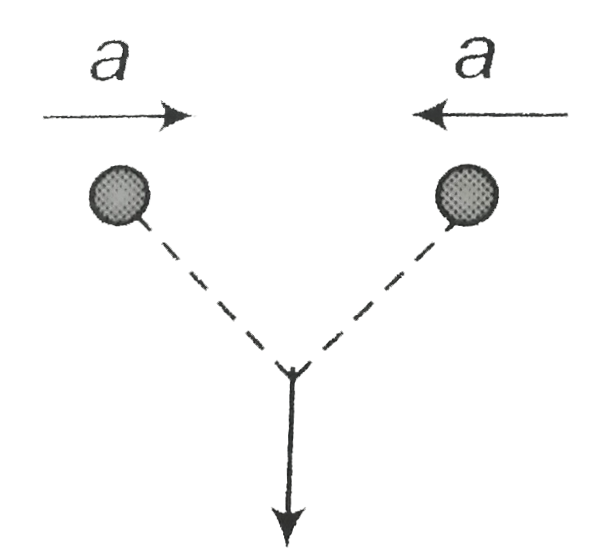 Acceleration of approach `h=a+a=2a`
Acceleration of approach `h=a+a=2a`