Home
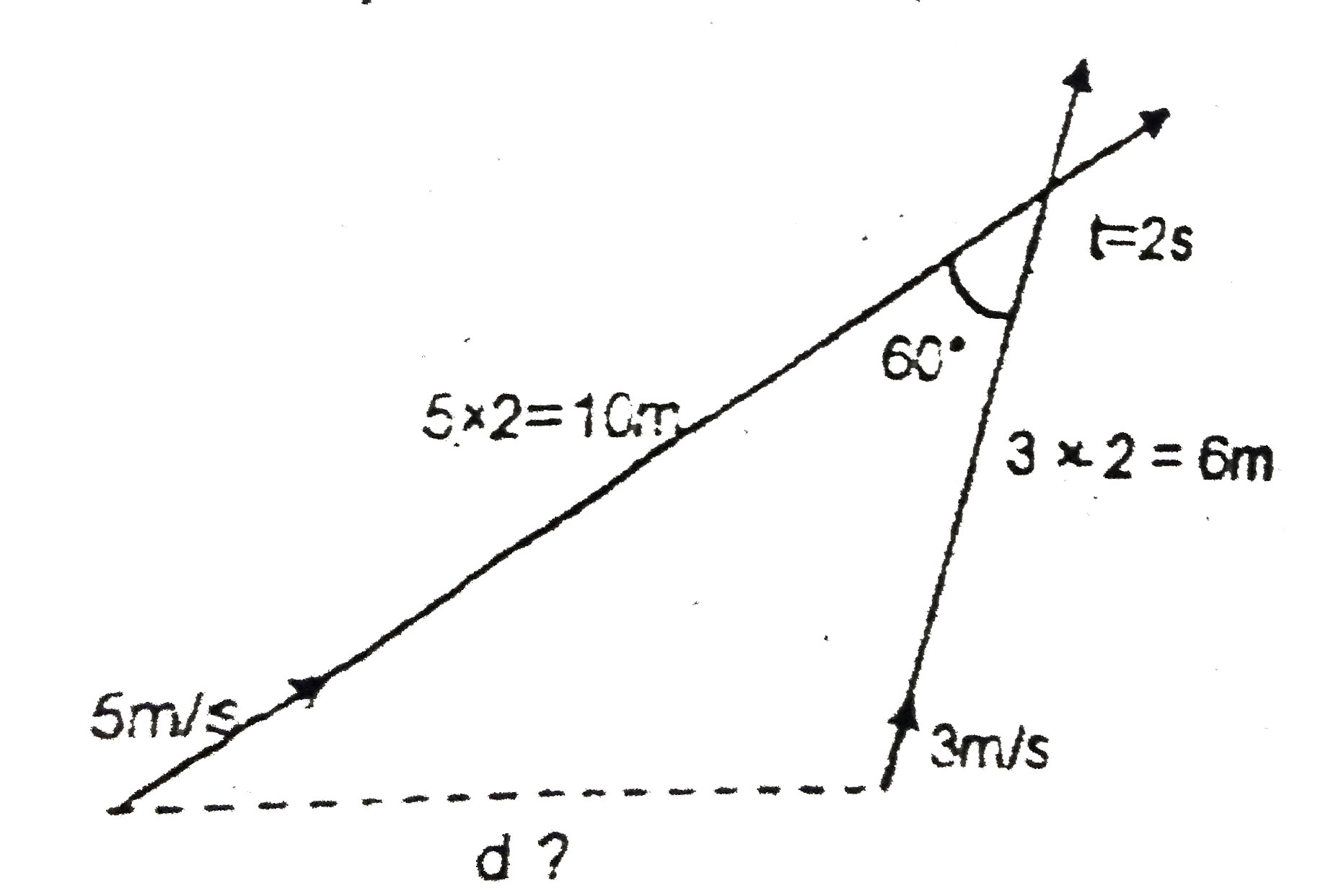
Class 12
PHYSICS
Two particles are intially at a separati...

Two particles are intially at a separation of d to each other. They move with constant velocirties with `5m//s` and `3m//s` respectively in horizontal plane. Their velocities makes an angle `60^(@)` with each other. If after 2 seconds, they collide. Then value of d is:

A

`2sqrt(19)m`

B

`8m`

C

`2m`

D

`32m`

Text Solution

Verified by Experts

The correct Answer is:
A
Two particlesw …………….. a

`cos 60^(@) = (10^(2)+6^(2)-d^(2))/(2xx10xx6)`
`(1)/(2) = (100+36-d^(2))/(120)`
`d = 2sqrt(19)`
Promotional Banner

Similar Questions

Explore conceptually related problems

Two particles are 100 m apart and start approaching each other with constant velocities of 2 m//s and 3 m//s . The particles will meet after.

Two balls of masses 10 kg and 20 kg approach each other with velocities 30 m/s and 20 m/s respectively . Calculate their velocities after they undergo a perfectly eleastic collision .

Two particles, one of mass m and the other of mass 2m, are projected horizontally towards each other from the same level above the ground with velocities 10 m/s and 5 m/s, respectively. They collide in air and stick to each other. The distance of the combined mass from point A is

Two balls of masses m each are moving at right angle to each other with velocities 6 m/s and 8 m/s respectively. If collision between them is perfectly inelastic, the velocity of combined mass is

two particles A and B are at separation of 100 m . They move towards each other with uniform speed, A with 5 m//s and B with 15 m//s . When and where the two particle meet?

Two equal masses m_1 and m_2 moving along the same straight line with velocites +3 m//s and - 5 m//s respectively collide elastically. Their velocities after the collision will be respectively.

Two perfectly elastic particles A and B of equal masses travelling along a line joining them with velocities 15 m//s and 10m//s respectively collide. Their velocities after the elastic collision will be (in m/s) respectively

A particle is projected with velocity 50 m/s at an angle 60^(@) with the horizontal from the ground. The time after which its velocity will make an angle 45^(@) with the horizontal is