Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
MOMENTUM AND CENTRE OF MASS
ARIHANT|Exercise Momentum And Center of Mass|117 VideosView PlaylistROTATIONAL MOTION
ARIHANT|Exercise PHYSICS|159 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
ARIHANT-NEWTONS LAWS OF MOTION-All Questions
- Three blocks A, B and C each of mass m are placed on a smooth horizont...
08:17
|
Play - A U shaped container has uniform cross sectional area S. It is suspend...
03:05
|
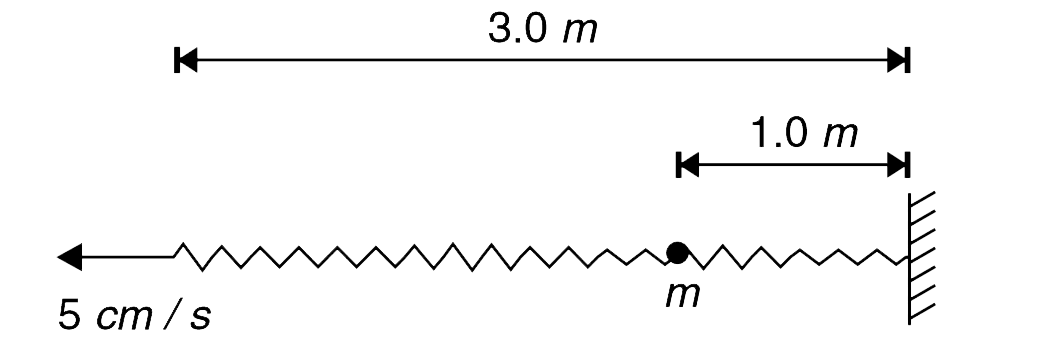
Play - A uniform light spring has unstretched length of 3.0 m. One of its end...
03:27
|
Playing Now - It was observed that a small block of mass m remains in equilibrium at...
05:10
|
Play - In an emergency situation while driving one has tendency to jam the br...
05:16
|
Play - A table cloth of length L is lying on a table with one of its end at t...
03:39
|
Play - A block rests on a horizontal surface. A horizontal force F is applied...
01:26
|
Play - Repeat the last problem if the graph is as shown below.
03:10
|
Play - In the system shown in the figure, the string is light and coefficient...
04:19
|
Play - A disc of mass m lies flat on a smooth horizontal table. A light strin...
02:36
|
Play - (i) A spinning disk has a hole at its centre. The surface of the disk ...
08:27
|
Play - Two particles of mass m(1) "and" m(2) are in space at separation vecr ...
03:34
|
Play - Six identical blocks – numbered 1 to 6 – have been glued in two groups...
05:40
|
Play - Two strange particles A and B in space, exert no force on each other w...
09:47
|
Play - A light string passing over a smooth pulley holds two identical bucket...
05:23
|
Play - A chain is lying on a smooth table with half its length hanging over t...
04:02
|
Play - A triangular wedge W having mass M is placed on an incline plane with ...
08:01
|
Play - In the system shown in fig, mass of the block is m(1) = 4 kg and that...
05:14
|
Play - A uniform chain of mass M = 4.8 kg hangs in vertical plane as shown in...
07:56
|
Play - Block A of mass M is placed on an incline plane, connected to a string...
04:36
|
Play