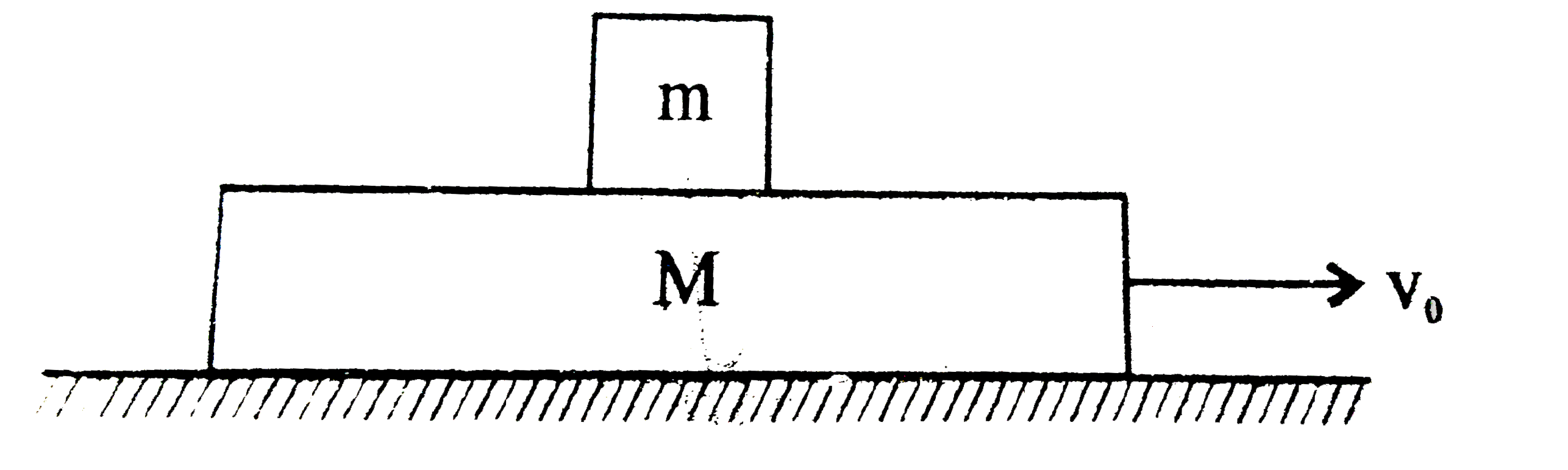Home
Class 12
PHYSICS
A block of mass m is placed gently onto ...

A block of mass m is placed gently onto a long plank of mass M moving with a velocity `v_(0)` on a smooth horizontal floor. If friction is present between M and m :

A

`v_("centre of mass") =(Mv_(0))/(M+m)`

B

`W_("friction")` on m is positive

C

`W_("Friction")` on M is negative

D

final velocity of both `= (mv_(0))/(m+M)`

Text Solution

Verified by Experts

The correct Answer is:
ABC
`v_(C)=(Mv_(0))/(M+m)`
`v_(5)=(Mv_(0))/(m+M)`
Promotional Banner

Topper's Solved these Questions

  • TEST PAPERS

    BANSAL|Exercise PHYSICS PART (A)|32 Videos

  • TEST PAPERS

    BANSAL|Exercise PHYSICS PART (B)|3 Videos

  • TEST PAPERS

    BANSAL|Exercise PHYSICS PART- C|4 Videos

  • SEMICONDUCTORS

    BANSAL|Exercise CBSE Question|32 Videos

Similar Questions

Explore conceptually related problems

A block A of mass m is placed over a plank B of mass 2m plank B is placed over a smooth horizontal surface .The coefficient of friction between A and B is 0.4 Block A is given a velocity v_(0) toward right Find acceleration (in ms^(-2) of B relative to A

A block A of mass m is placed over a plank B of mass 2m. Plank B is placed over a smooth horizontal surface. The coefficient of friction between A and B is (1)/(2) block A is given a velocity v_(0) towards right. Accelration of B relative to A is

A block of mass m moving with velocity v_(0) on a smooth horizontal surface hits the spring of constant k as shown. Two maximum compression in spring is

A block of mass m is placed at rest on a smooth wedge of mass M placed at rest on a smooth horizontal surface. As the system is released

A bar of mass m_(1) is placed on a plank of mass m_(2) which rests on a smooth horizontal plane . The coefficient of friction between the surfaces of bar and plank is k . The plank is subjected to a horizontal force F depending on time t as F = at , where a is a constant . The moment of time t_(0) at which the plank starts sliding is :

A bolck of mass m =2 kg is placed on a plank of mass M = 10 kg, which is placed on a smooth horizontal plane as shown in the figure. The coefficient of friction between the block and the plank is mu=(1)/(3) . If a horizontal force F is applied on the plank, then the maximum value of F for which the block and the plank move together is (g=10m//s^(2))

A block of mass m=2kg of shown dimensions is placed on a plank of mass M = 6Kg which is placed on smooth horizontal plane. The coefficient of friction between the block and the plank is mu=1/3 . If a horizontal froce F is applied on the plank, then find the maximum value of F (in N) for which the block and the plank move together

The block of mass m is kept on plank of mass M. The block is given velocity V_(0) as shown. The coefficient of friction between the block of mass m and plank of mass M is mu and its value is such that block becomes stationary with respect to plank before it reaches the other end. Then:

A block A of mass m is over a plank B of mass 2m . Plank B si placed over a smooth horizontal surface. The coefficient of friction between A and B is (1)/(2) . Blocks A is given a velocity V_(0) towards right. Then

A cylinder of mass m is placed on the edge of a long plank of same mass kept on the smooth horizontal surface, where mu the is the coefficient of friction between cylinder and plank. The cylinder is given an impulse at t=0 which impacts it is velocity V_(0) . find the time in which pure rolling starts.

BANSAL-TEST PAPERS-PHYSICS
  1. A cuboid of height 10 cm, width 5 cm and 8 kg is kept on a rough horiz...

    Text Solution

    |

  2. A small particle starts moving from point P along the smooth inclined ...

    Text Solution

    |

  3. A block of mass m is placed gently onto a long plank of mass M moving ...

    Text Solution

    |

  4. In which of the following cases, the moment of inertial is greater tha...

    Text Solution

    |

  5. In each of the following situations, comment on the force F direction.

    Text Solution

    |

  6. Each propeller on a King Air twin-engine airplane consists of three bl...

    Text Solution

    |

  7. An empty box of mass 5kg is found to accelerate up at the rate of g/6 ...

    Text Solution

    |

  8. A rocket of initial mass m ( including fuel) ejects mass at a constant...

    Text Solution

    |

  9. A bullet of mass m=10 gm strikes a hanging block of mass M=50 gm inela...

    Text Solution

    |

  10. One end of a light rod of length 1m is attached with a string of lengt...

    Text Solution

    |

  11. AB is an L shaped obstacle fixed on a horizontal smooth table. A ball ...

    Text Solution

    |

  12. A uniform rod of mass m and length L lies radialy on a disc rotating w...

    Text Solution

    |

  13. Two identical uniform discs of mass m and radius r are arranged as sho...

    Text Solution

    |

  14. A particle moves in a straight line with retardation proportional to i...

    Text Solution

    |

  15. A machine gun fires a bullet of mass 40 g with a velocity 1200 ms^-1. ...

    Text Solution

    |

  16. A particles of mass m is fixed to one end of a light spring of force c...

    Text Solution

    |

  17. The upper half of an inclined plane with inclination phi is perfectly ...

    Text Solution

    |

  18. The relation between time t and distance x is t = ax^(2)+ bx where a a...

    Text Solution

    |

  19. A cone of mass m falls from a height h and penetrates into sand. The r...

    Text Solution

    |

  20. A ball is projected towards right from point A at an angle theta with ...

    Text Solution

    |