A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
TEST PAPER
ALLEN|Exercise PHYSICS|4 VideosView PlaylistTEST PAPER
ALLEN|Exercise PHYSICS|4 VideosView PlaylistSIMPLE HARMONIC MOTION
ALLEN|Exercise Example|1 VideosView PlaylistTEST PAPER 1
ALLEN|Exercise PHYSICS|11 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
ALLEN-TEST PAPER-Exercise (Physics)
- A particle is thrown vertically upward with a speed u from the top of ...
02:46
|
Play - Find the x coordinate of the centre of mass of the bricks shown in fig...
04:54
|
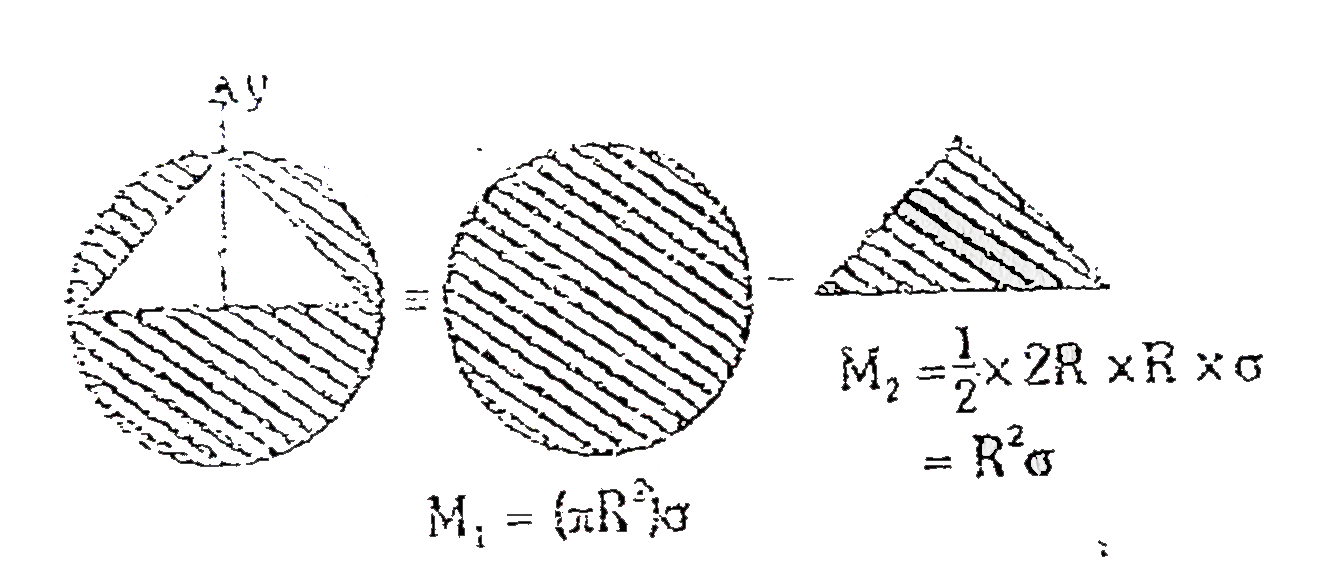
Play - From a circular disc of radius R, a triangular portion is cut (sec fig...
04:46
|
Playing Now - A sector cut from a uniform disk of radius 12cm and a uniform rod of t...
03:01
|
Play - Mass centers of a system of three particles of masses 1,2,3kg is at th...
05:08
|
Play - A machinist starts with three identical square plates but cuts one cor...
01:05
|
Play - Pull down in the middle a heavy chain, fixed at both ends, in such a w...
01:32
|
Play - Particle of masses m, 2m,3m,…,nm grams are placed on the same line at ...
02:58
|
Play - To form a jeep, two squares of side length 10cm & 20cm and two circles...
Text Solution
|
Play - Three rods of the same mass are placed as shown in the figure. Calcula...
01:51
|
Play - A uniform wire frame ABC is in the shape of an equilateral triangle in...
01:50
|
Play - The figure below depicts the paths of two colliding steel balls, A and...
01:33
|
Play - A uniform chain of mass m and length l hangs on a thread and touches t...
03:48
|
Play - Two forces F(1) and F(2) are applied simultaneously on a 2kg block res...
07:24
|
Play - A 6.0kg mass is moving to the right at 10 m//s. A 0.25kg mass is fired...
01:17
|
Play - Two identical balls moving in opposite directions in free space collid...
02:13
|
Play - In figure, determine the character of the collision. The masses of the...
03:40
|
Play - A rod has non uniform mass distribution. The mass increases uniformly ...
01:41
|
Play - A solid hemisphere and a hemisphereical shell are joined as shown. Bot...
03:19
|
Play - In a system of four thin uniform rods are each of mass inas shown. If ...
02:52
|
Play