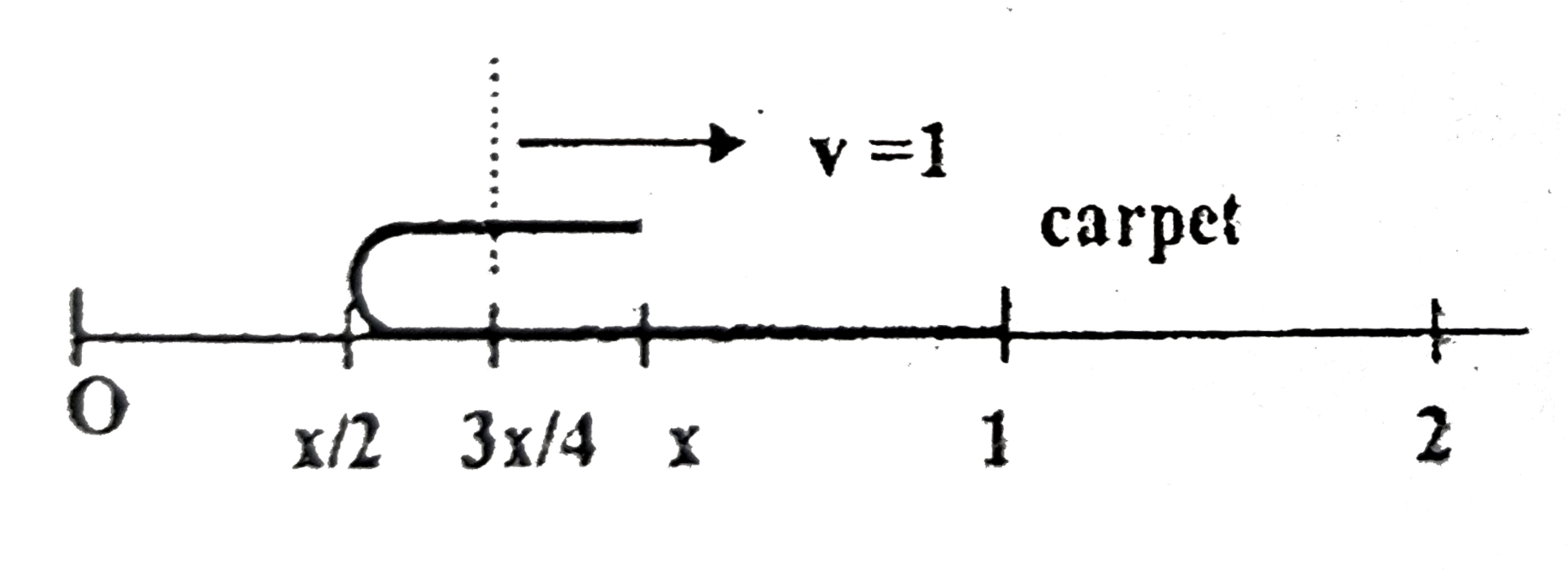Text Solution
Verified by Experts
|
Topper's Solved these Questions
ELASTICITY & WAVES
FIITJEE|Exercise Example|16 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
FIITJEE-CONSERVATION OF MOMENTUM-Example
- A carpet of unit mass an unit length is laid on the floor. One end of ...
04:16
|
Playing Now - PQR is a wedge fixed to the floor. Two blocks A & B of equal mass m=1k...
06:47
|
Play - An elastic ball of mass 'm' is suspended from a fixed point by an inex...
04:29
|
Play - A ball is projected from a point in a horizontal plane so as to strike...
05:18
|
Play - A tiny ball of mass m is released from the state of rest over a large ...
14:35
|
Play - A point objects of mass m is slipping down on a smooth hemispherical b...
06:15
|
Play - An iron ball of mass m, suspended by a light inextensible string of le...
10:46
|
Play - A particle of mass m is released from height h on smooth quarter circu...
01:09
|
Play - A ping-pong ball of mass m is floating in air by a jet of water emergi...
02:36
|
Play - A block of mass m is pushed towards a movable wedge of mass nm and hei...
05:48
|
Play - A circular are (AB) of thin wire frame of radius R and mass M makes an...
02:13
|
Play - From a 16cmxx8cm rectangular uniform plane sheet, exactly one quarter ...
02:07
|
Play - A block B is at rest on the rough horizontal surface as shown. Another...
01:29
|
Play - Infinite number of bricks are placed one over the other as shown in th...
07:14
|
Play - A particle strikes a smooth horizontal surface at an angle of 45^(@) w...
02:15
|
Play