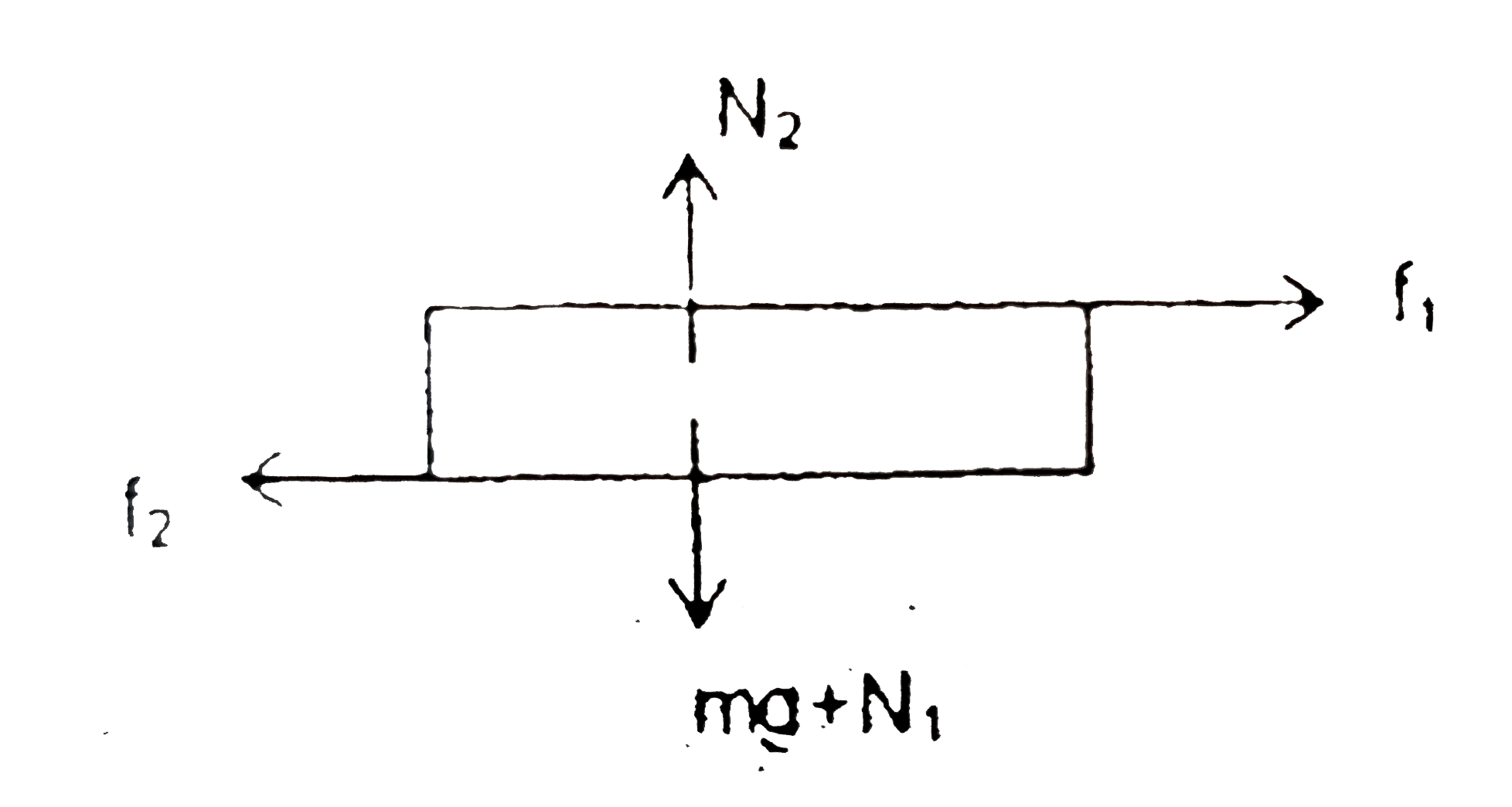
Text Solution
Verified by Experts
|
Topper's Solved these Questions
LAWS OF MOTION
FIITJEE|Exercise Example|12 VideosView PlaylistSIMPLE HARMONIC MOTION
FIITJEE|Exercise Example|15 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
FIITJEE-ROTATIONAL MECHANICS-Example
- In the figure shown, a solid sphere of mass 'm' and radius r is releas...
08:05
|
Playing Now - A cube of side a and mass M is pivoted on a horizontal axis such that ...
10:55
|
Play - A spool of thread of mass m and moment of inertia I is attached to the...
12:53
|
Play - A sphere of radius R is projected with a reverse spin omega(0) down a ...
05:14
|
Play - A plank of mass M is moving on a smooth horizontal surface with speed ...
07:51
|
Play - A solid sphere is rolling on a rough surface, whose centre of mass is ...
02:17
|
Play - When a body rolls without sliding up an inclined plane the frictional ...
01:41
|
Play - A particle m starts with zero velocity along a line y=4d. The position...
01:28
|
Play - A sphere of radius R and mass M collides elastically with a cubical bl...
01:57
|
Play - A body of mass m and radius r is released from rest along a smooth inc...
02:05
|
Play - Ler l be the moment of inertia of a uniform square plate about an axi...
01:26
|
Play - When a car negotiates a curve, the normal force exerted on the inner a...
02:48
|
Play - A massless string is wrapped around a hollow cylinder having mass m an...
01:42
|
Play - A cubical box of side length L rests on a rough horizontal surface hav...
02:19
|
Play - Two identical unifrom rods OA and OB each of length l and mass m are c...
04:01
|
Play - Two identical unifrom rods OA and OB each of length l and mass m are c...
04:01
|
Play - Two identical unifrom rods OA and OB each of length l and mass m are c...
04:01
|
Play