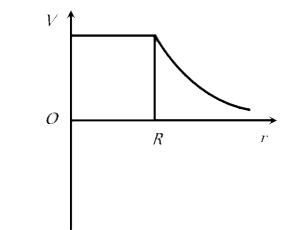
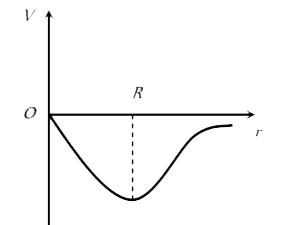
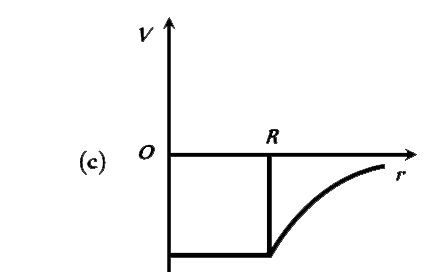
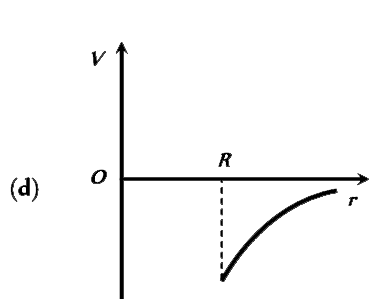
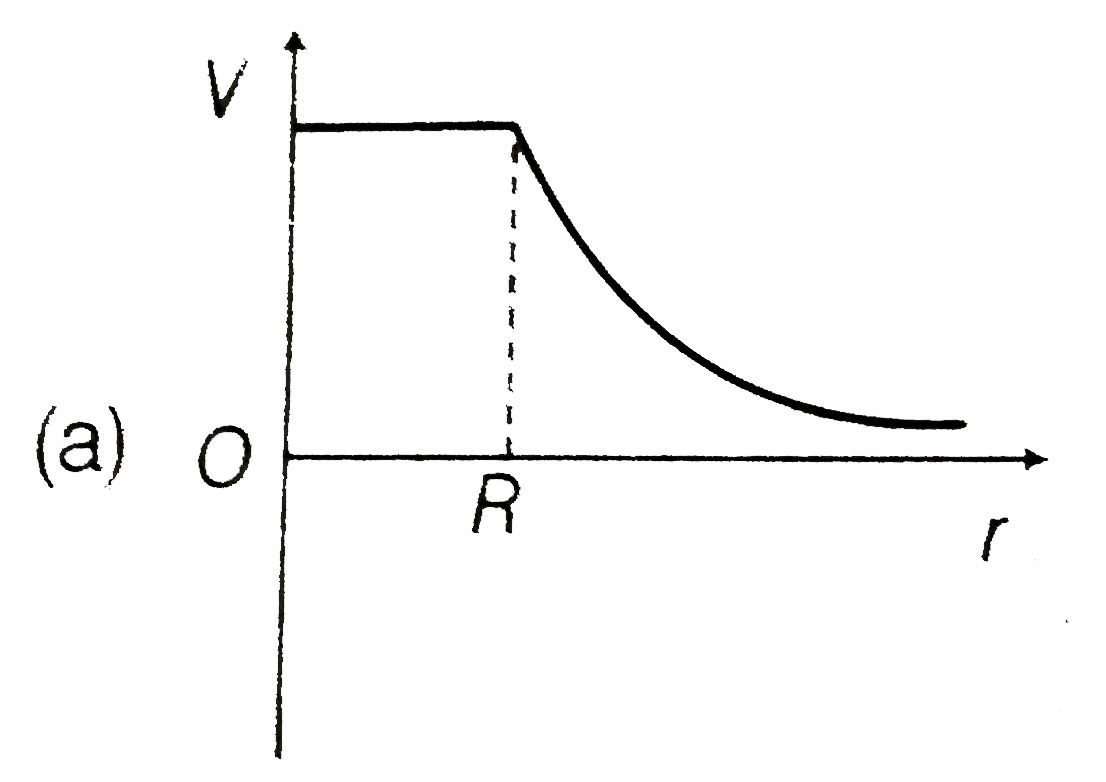
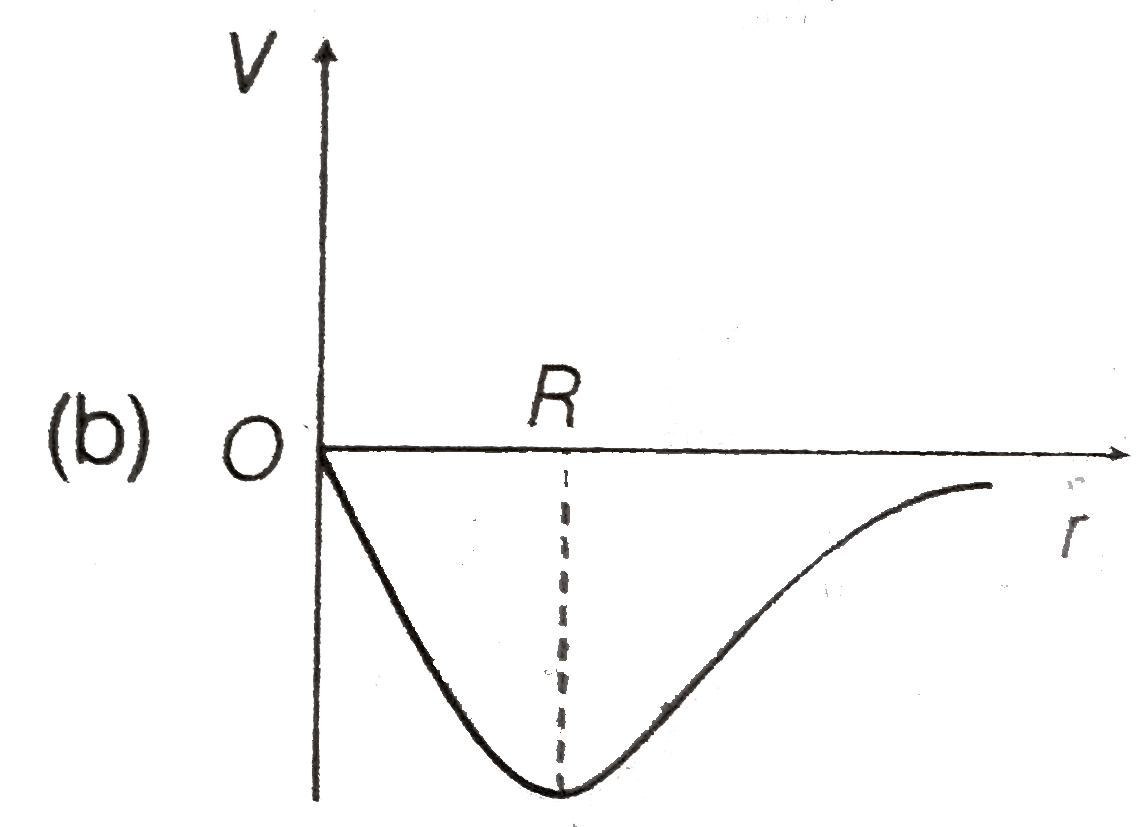
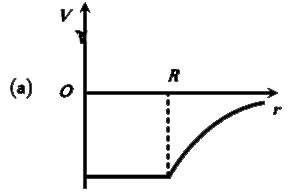
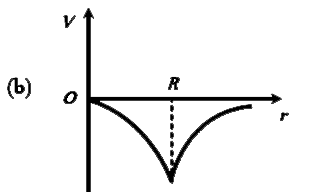
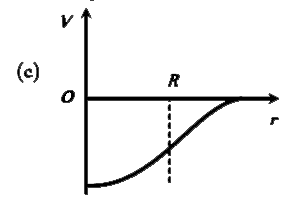
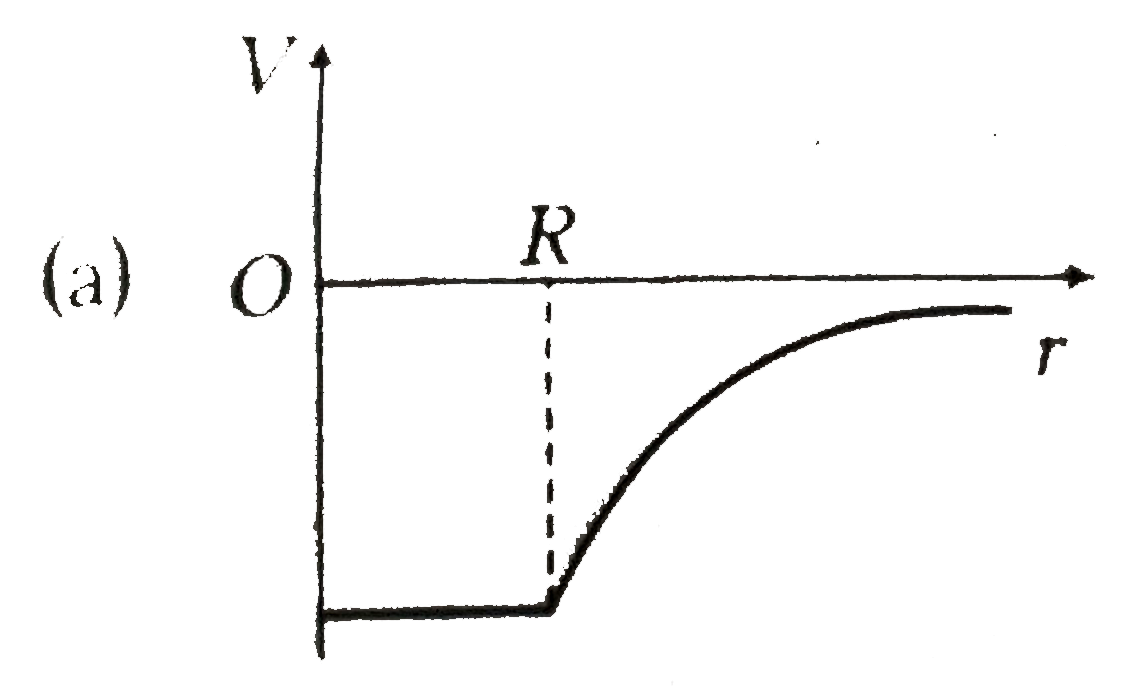
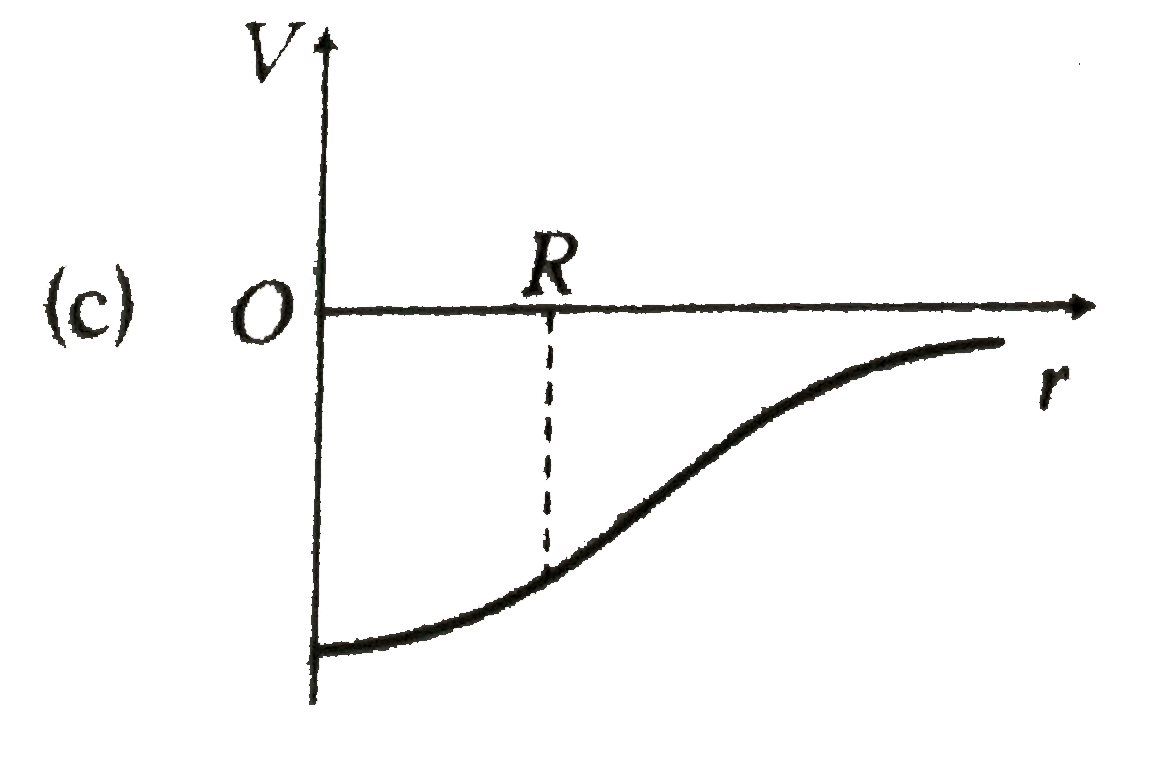
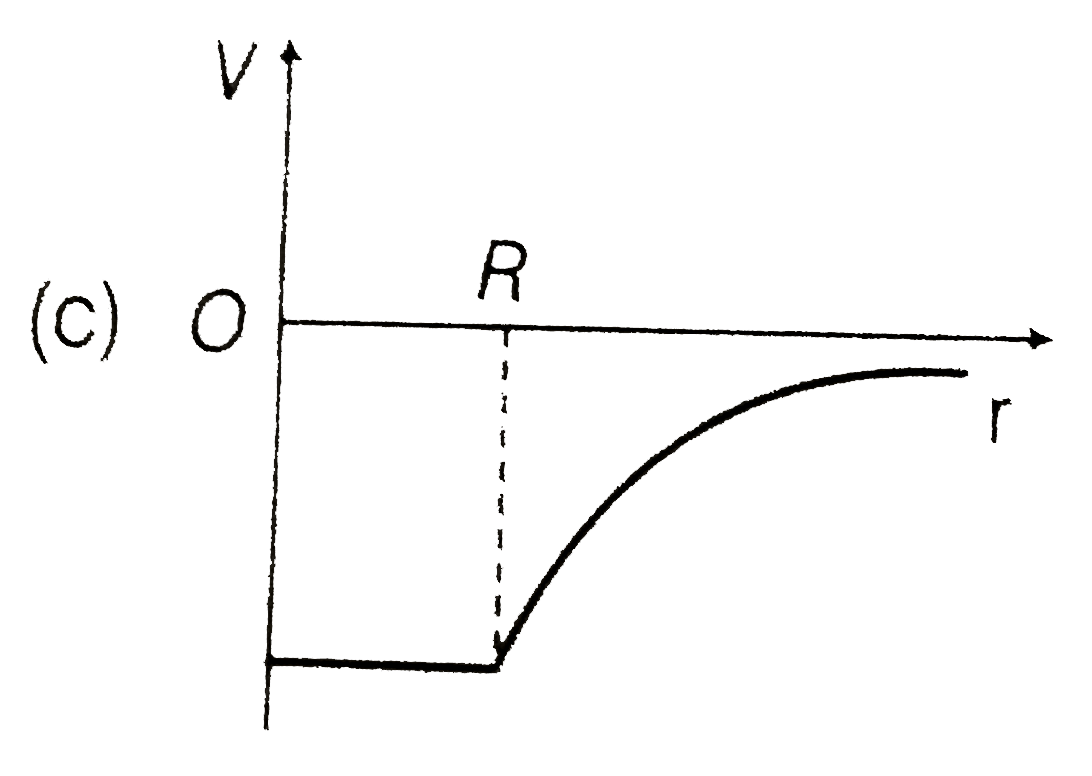A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
|
Topper's Solved these Questions
GRAVITATION
ERRORLESS |Exercise Assertion and Reasons|33 VideosView PlaylistGRAVITATION
ERRORLESS |Exercise SET|27 VideosView PlaylistGRAVITATION
ERRORLESS |Exercise CT|18 VideosView PlaylistFRICTION
ERRORLESS |Exercise MCQ S|125 VideosView PlaylistMOTION IN ONE DIMENSION
ERRORLESS |Exercise Motion In One Dimension|24 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
ERRORLESS -GRAVITATION-GQ
- Assuming the earth to have a constant density, point out which of the ...
02:44
|
Play - The diagram showing the variation of gravitational potential of earth ...
04:10
|
Play - By which curve will the variation of gravitational potential of a holl...
02:52
|
Playing Now - A cavity of radius R//2 is made inside a solid sphere of radius R. The...
08:25
|
Play - Which one of the following plots represents the variation of the gravi...
01:48
|
Play - Suppose the acceleration due to gravity at earth's surface is 10ms^-2 ...
02:38
|
Play - Which of the following graphs represents the motion of the planet movi...
01:22
|
Play - The curves for potential energy ( U ) and kinetic energy (E(k)) of a t...
02:04
|
Play - The correct graph representing the variation of total energy (E(t)), k...
02:43
|
Play - A shell of mass M and radius R has point mass m placed at a distance r...
02:31
|
Play