Five equal resistances each of value R ...

Five equal resistances each of value R are connected in a form shown alongside. The equivalent resistance of the network

A

Between the points B and D is R

B

Between the points B and D is `(R)/(2)`

C

Between the points A and C is R

D

Between the points A and C is `(R)/(2)`

Text Solution

Verified by Experts

The correct Answer is:

B, C

Topper's Solved these Questions

CURRENT ELECTRICITY
ERRORLESS |Exercise Kirchhoff s Law, cells|8 Videos
CURRENT ELECTRICITY
ERRORLESS |Exercise Different Measuring Instruments|1 Videos
COMMUNICATION SYSTEM
ERRORLESS |Exercise S E T|14 Videos
ELECTRO MAGNETIC INDUCTION
ERRORLESS |Exercise SET|20 Videos

Similar Questions

Explore conceptually related problems

Five equal resistances each of value R are connected in a form shown in the following figure. The equivalent resistance of the network

Three equal resistances each of value R are joined as shown in the figure. The equivalent resistance between M and N is

Twelve equal resistors each R Omega are connected to from the edges of a cube . Find the equivalent resistance of the network. When current enters at 1 and leaves at 3

Twelve equal resistors each R Omega are connected to from the edges of a cube . Find the equivalent resistance of the network. When current enters at 1 and leaves at 2

Five equal resistors each of R Omega are connected in a network. Calculate the equivalent resistance between the points A and B.

Three resistors each of 4 Omega are connected together to form a network. The equivalent resistance of the network cannot be

Eight resistances each of resistance 5 Omega are connected in the circuit as shown in figure. The equivalent resistance between A and B is

Six resistors each of resistance R and two resistors each of resistance r are connected in the network shown below. The equivalent resistance between A and B is

Inside a supeerconducting ring, six identical resistors each of resistance R are connected as shown in figure. The equivalent resistances.

ERRORLESS -CURRENT ELECTRICITY-Self Evaluation Test -19

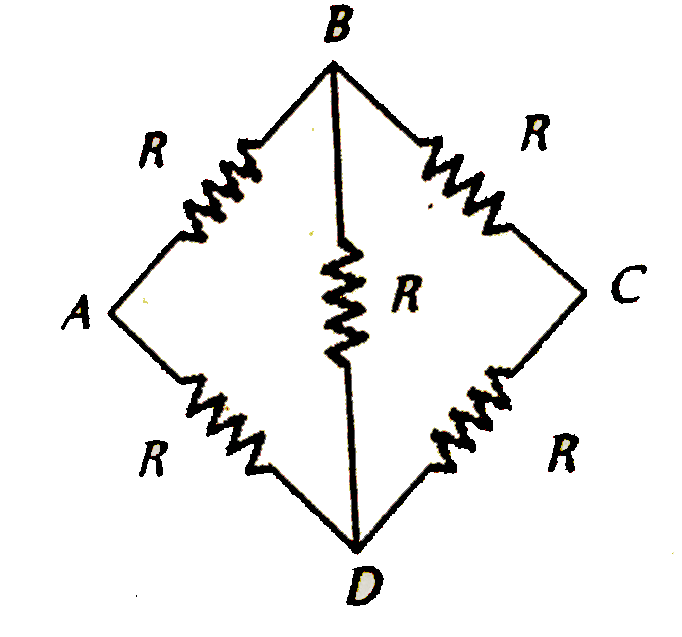
Five equal resistances each of value R are connected in a form shown ...
Text Solution
|
Figure 6.51 shows a simple a potentiometer circuit for measuring a sma...
Text Solution
|
A car has a fresh storage battery of emf 12 V and internal resistance ...
Text Solution
|
If the balance point is obtained at the 35th cm in a metre bridge the ...
Text Solution
|
The equivalent resistance across the terminals of source of e.m.f. 24 ...
Text Solution
|
In the circuit shown in figure, switch S is initially closed and S i...
Text Solution
|
The figure here shows a portion of a circuit. What are the magnitude a...
Text Solution
|
A carbon resistor has colour strips as violet, yellow brown and golden...
Text Solution
|
A voltmeter of resistance 1000 Omega is connected across a resistance ...
Text Solution
|
A beam contains 2 xx 10^(8) doubly charged positive ions per cubic cen...
Text Solution
|
In the circuit shown, the reading of ammeter when switch S is open ...
Text Solution
|
In the circuit as shown in figure the
Text Solution
|
In figure shows a rectangular block with dimensions x , 2 x and 4 x ....
Text Solution
|
A battery is connected to a uniform resistance wire AB and B is eart...
Text Solution
|
A cylindrical metal wire of length l and cross sections area S , has...
Text Solution
|
A potential divider is used to give outputs of 4 V and 8 V from a 12 V...
Text Solution
|
Find equivalent resistance between A and B
Text Solution
|
Following figures show four situations in which positive and negative ...
Text Solution
|
A and B are two square plates of same metal and same thickness but len...
Text Solution
|
A moving coil galvanometer is converted into an ammeter reads upto 0.0...
Text Solution
|
Two conductors are made of the same material and have the same length....
Text Solution
|