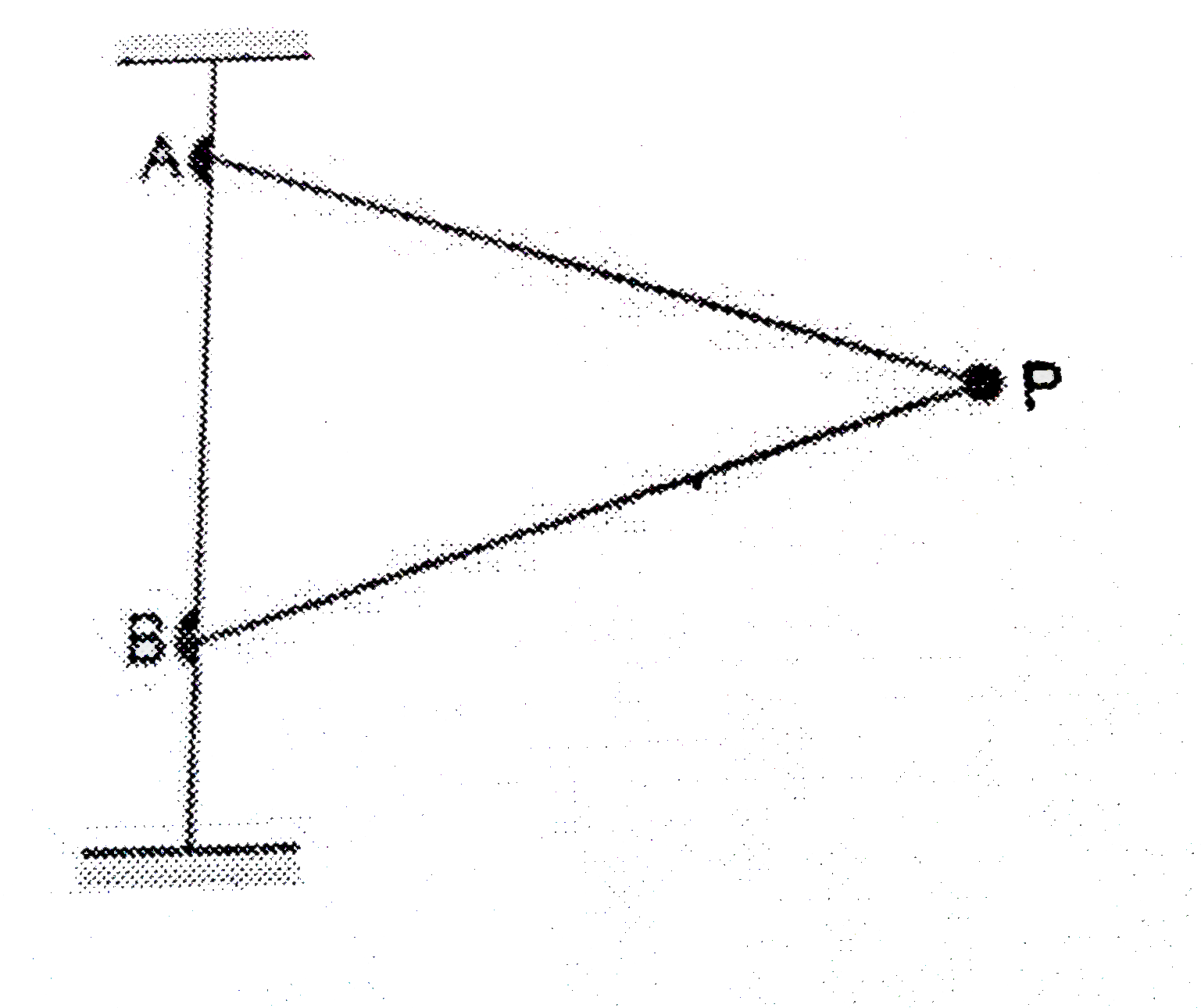A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
MISCELLANEOUS QUESTION 2
D MUKHERJEE|Exercise Missellaneous Qns-2 (Assertion)|25 VideosView PlaylistMISCELLANEOUS QUESTION 4
D MUKHERJEE|Exercise Missellaneous Qns-4 (Matrix Matching Type)|9 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
D MUKHERJEE-MISCELLANEOUS QUESTION 3-Missellaneous Qns-3 (Pragraph)
- The particle P of mass m is attached to two light, rigid rods AP and B...
05:14
|
Playing Now - The particle P of mass m is attached to two light, rigid rods AP and B...
Text Solution
|
Play - The particle P of mass m is attached to two light, rigid rods AP and B...
Text Solution
|
Play - In a ring ABCD of radius r, the lower half ABC has mass m and the uppe...
Text Solution
|
Play - In a ring ABCD of radius r, the lower half ABC has mass m and the uppe...
Text Solution
|
Play - In a ring ABCD of radius r, the lower half ABC has mass m and the uppe...
Text Solution
|
Play - A biconvex lens made of material with refractive index n(2). The radii...
06:07
|
Play - A biconvex lens made of material with refractive index n(2). The radii...
Text Solution
|
Play - A biconvex lens made of material with refractive index n(2). The radii...
Text Solution
|
Play - Electrical multimeters, or multitesters, are widely used by technician...
Text Solution
|
Play - Electrical multimeters, or multitesters, are widely used by technician...
Text Solution
|
Play - Electrical multimeters, or multitesters, are widely used by technician...
Text Solution
|
Play - The figure shows three identical parallel conducting plates X, Y and Z...
Text Solution
|
Play - The figure shows three identical parallel conducting plates X, Y and Z...
Text Solution
|
Play - The figure shows three identical parallel conducting plates X, Y and Z...
Text Solution
|
Play - The diagram shows the basic setup for the production of X-rays. A(1) a...
Text Solution
|
Play - The diagram shows the basic setup for the production of X-rays. A(1) a...
Text Solution
|
Play - The diagram shows the basic setup for the production of X-rays. A(1) a...
Text Solution
|
Play