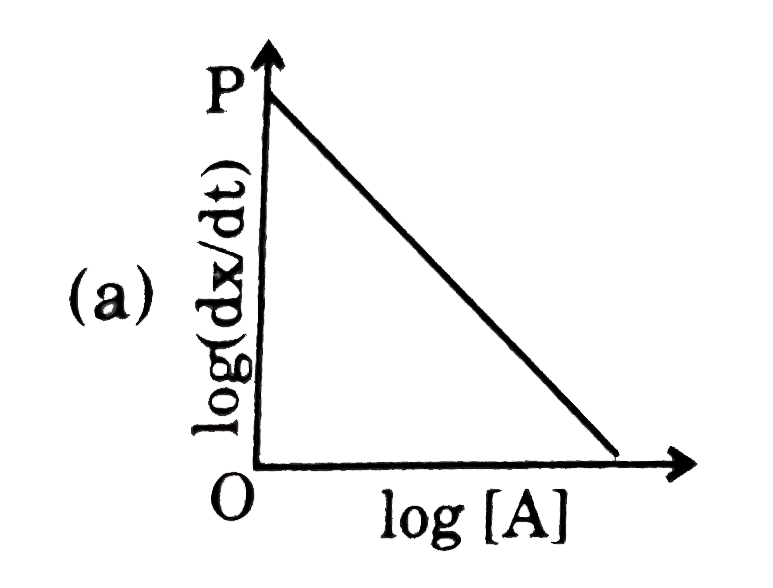
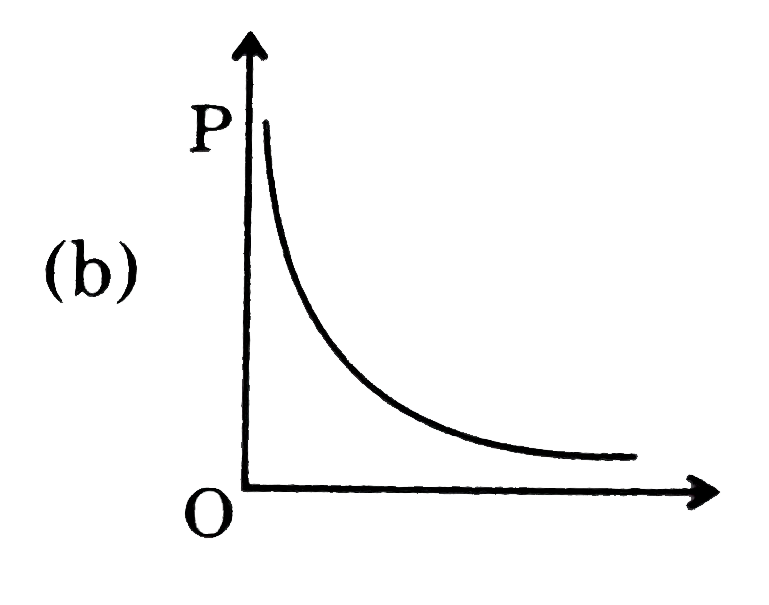
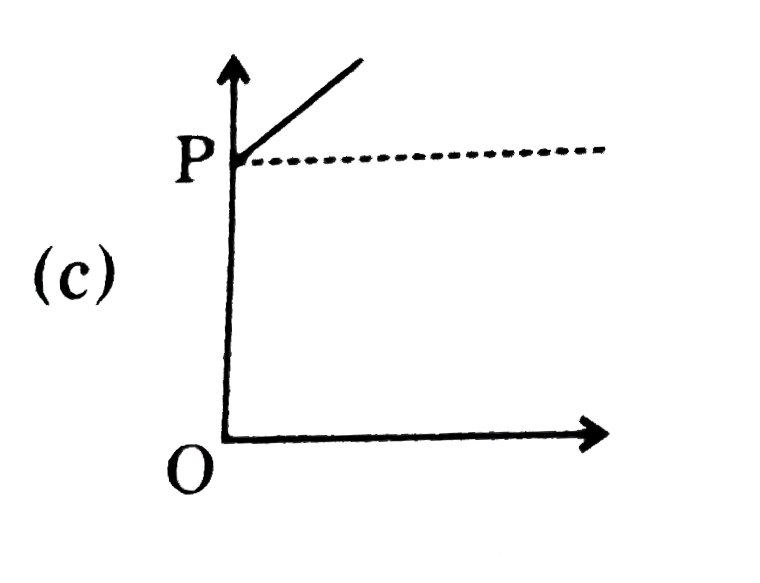
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
|
Topper's Solved these Questions
GRAPHICAL INTERPRETATION
GRB PUBLICATION|Exercise I.Electrochemistry|1 VideosView PlaylistGRAPHICAL INTERPRETATION
GRB PUBLICATION|Exercise Electrochemistry|9 VideosView PlaylistGRAPHICAL INTERPRETATION
GRB PUBLICATION|Exercise H. Chemical Kinetics|1 VideosView PlaylistF-BLOCK ELEMENTS
GRB PUBLICATION|Exercise Subjective type|7 VideosView PlaylistHYDROCARBON (ALIPHATIC)
GRB PUBLICATION|Exercise Previous years jee questions|28 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
GRB PUBLICATION-GRAPHICAL INTERPRETATION-Chemical Kinetics
- A graph plotted between log t(50%) vs log concentration is a straight ...
01:38
|
Play - What will be the order of reaction and rate constant for a chemical ch...
06:14
|
Play - A rarr Product and ((dx)/(dt)) = k [A]^(2). If log ((dx)/(dt)) is plot...
01:59
|
Playing Now - In the different reactions, involving a angle reactant in each case, a...
01:53
|
Play - The Arrhenius relationship of two different reactions is shown below. ...
03:27
|
Play - If for a reaction in which A(g) converts to B(g) the reaction carried ...
01:50
|
Play - Rate of reaction A rarr B depends only on A and can be represented by ...
03:32
|
Play - Adjoining graph is for a reaction which have only single reactant (R) ...
01:35
|
Play - The conversion of vinyl allyl ether to pent-4-enol follows first-order...
02:24
|
Play - A simple mechanism for enzyme-catalysed reaction is given by the follo...
02:35
|
Play - In the following graphical representation for the reaction A rarr B th...
03:28
|
Play - Rate law of the reaction A rarr Product is, rate = k[A]. Graphically i...
01:06
|
Play - Which graph is diagnostic of an irreversible second order reaction A r...
02:47
|
Play - For the reaction A rarr B, what is the order with respect to A that gi...
02:37
|
Play - Which of the reactions represented in these diagrams will show the gre...
03:04
|
Play - What names apply to chemical species corresponding to locations 1 and ...
01:47
|
Play - How can be rate of reaction at a specific in the be determined from a ...
03:24
|
Play - If a reaction A rarr B has the rate low k[A],which graph produced a st...
02:48
|
Play - Following reaction can take place in both direction A overset(k(1))und...
03:39
|
Play - Graph between log k and (1)/(T) (k is rate constant in s^(-1) and T is...
03:17
|
Play