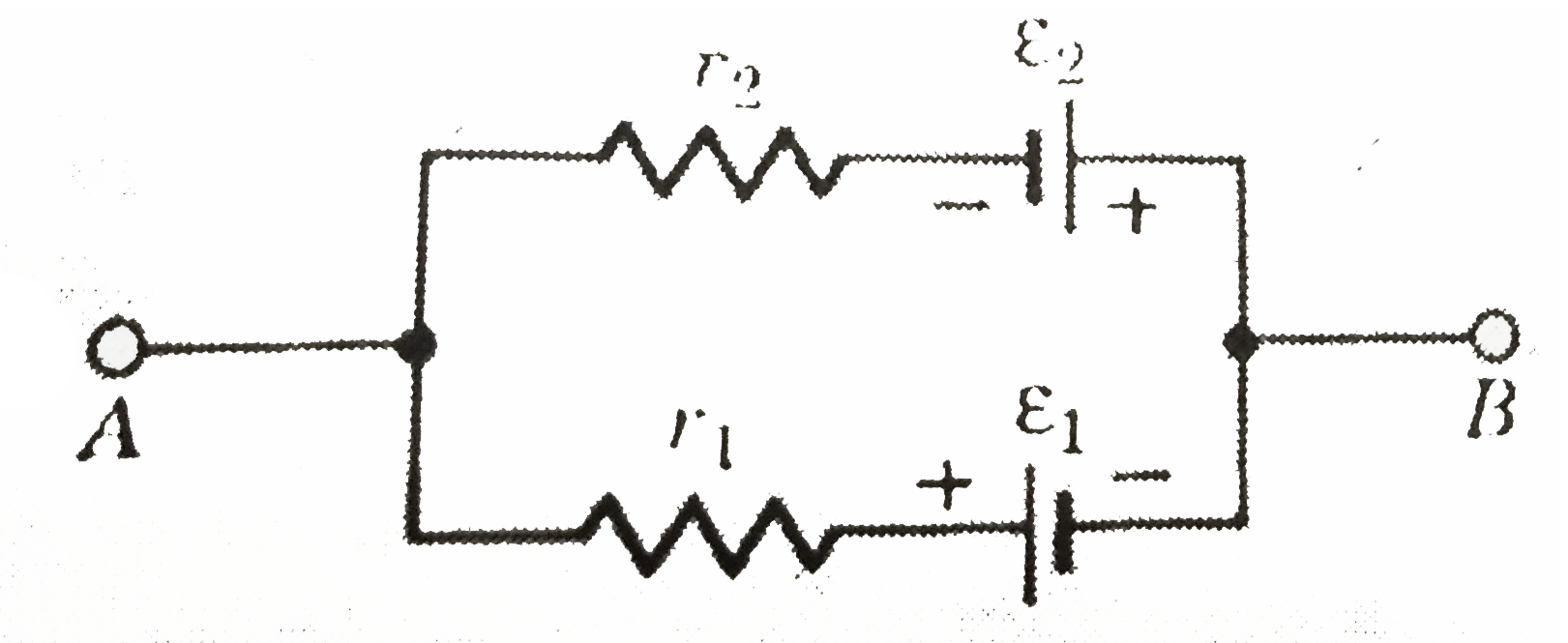Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
ELECTRICAL INSTRUMENTS
SL ARORA|Exercise Problem From competitive examinations|11 VideosView PlaylistELECTRIC POTENTIAL AND ELECTRIC FLUX
SL ARORA|Exercise Problems for self practive|61 VideosView PlaylistELECTROMAGNETIC INDUCTION
SL ARORA|Exercise All Questions|108 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
SL ARORA-ELECTRICAL INSTRUMENTS-Problem for self practice
- Compute the values of i(1),i(2),i(3) and V in the circuit, shown in fi...
Text Solution
|
Play - A certain length of a uniform wire of resistance 12Omega is bent into ...
Text Solution
|
Play - find the emf (epsi(0)) and internal resistance (r(0)) if a battery whi...
Text Solution
|
Playing Now - In figure. ABCDA is a uniform circular wire of resistance 2Omega,AOC a...
Text Solution
|
Play - Three batteries of emf 4,5 and 6V and internal resistances 1,2 and 3Om...
Text Solution
|
Play - One ampere of current enters the junction A of a wheatstone bridge ABC...
Text Solution
|
Play - In the circuit shown in figure. Find the currents I,I(1),I(2) and I(3)...
Text Solution
|
Play - Determine the current flowing through the galvanometer G of the Wheats...
Text Solution
|
Play - A current of 0.1 A enters a Wheatstone bridge consisting of three arms...
06:43
|
Play - The terminals of a battery of emf 3 V and internal resistance 2.5Omega...
04:43
|
Play - Twelve identical wires each of resistance 6 Omega are arranged to from...
02:10
|
Play - Twelve equal wires each of resistance r Omega form a cube. The effect...
15:17
|
Play - A galvanometer has a resistance of 49Omega.If 2% of the main current i...
01:22
|
Play - how will you convert a 1mA full scale deflection meter of resistance 1...
02:36
|
Play - Calculate the value of resistance needed to convert a galvanometer of ...
02:16
|
Play - A galvanometer with a coil of resistance 10.0Omega shows full scale de...
Text Solution
|
Play - A galvanometer has an internal resistance 1.0Omega. It given maximum d...
Text Solution
|
Play - A galvanometer has a resistance of 15.0Omega and the meter shows full ...
Text Solution
|
Play - In galvanometer of resistance 20Omega gives a deflection of one divisi...
Text Solution
|
Play - In a galvanometer there is a deflection of one divisions per mA. The i...
Text Solution
|
Play