A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
ROTATION
DC PANDEY|Exercise (B) Chapter Exercises|25 VideosView PlaylistRAY OPTICS
DC PANDEY|Exercise Integer type q.|15 VideosView PlaylistROTATIONAL MECHANICS
DC PANDEY|Exercise Subjective Questions|2 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
DC PANDEY-ROTATION-(C) Chapter Exercises
- Two bodies have their moments of inertia I and 2I, respectively about ...
Text Solution
|
Play - A body having a moment of inertia about its axis of rotation equal to ...
Text Solution
|
Play - A uniform solid spherical ball is rolling down a smooth inclined plane...
Text Solution
|
Play - A rod PQ of mass M and length L is hinged at end P. The rod is kept ho...
Text Solution
|
Play - A small object of uniform density rolls up a curved surface with an in...
Text Solution
|
Play - The conservation of angular momentum demands that
02:06
|
Play - The moment of inertia (I) and the angular momentum (L) are related by ...
02:23
|
Play - The moment of ineria (I) of a sphere of radius R and mass M is given b...
01:54
|
Play - A particle mass m is attached to a thin uniform rod of length a at a d...
02:44
|
Play - A particle moving in a circular path has an angular momentum of L. If ...
Text Solution
|
Play - The torque of a force F = 2 hat(i) - 3 hat(j) +5 hat(k) acting at a po...
02:38
|
Play - Moment of inertia of a disc of radius R about a diametric axis is 35 "...
Text Solution
|
Play - A wheel having moment of inertia 2 "kg-m"^(2) about its vertical axis,...
Text Solution
|
Play - What is the moment of inertia of solid sphere of density rho and radiu...
Text Solution
|
Play - The radius of gyration of a body depends upon
01:21
|
Play - Two discs have same mass and thickness. Their materials are of densiti...
02:44
|
Play - If a disc starting from rest acquires an angular velocity of 240 "rev ...
01:49
|
Play - A thin hollow sphere of mass m is completely filled with a liquid of m...
03:34
|
Play - The moment of inertia of a circular loop of radius R, at a distance of...
03:45
|
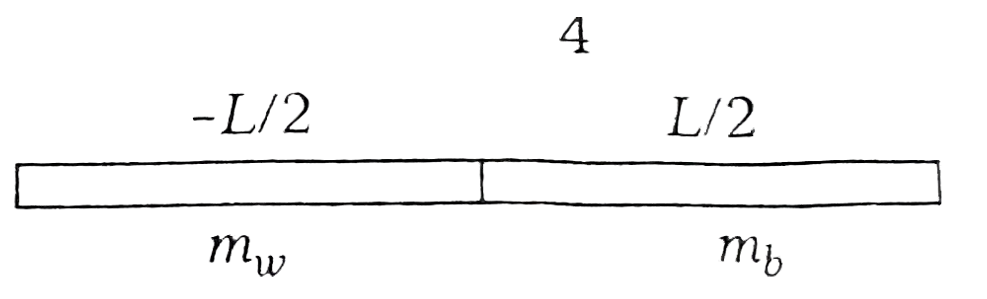
Play - A rod of length L is composed of a uniform length 1/2 L of wood mass i...
03:01
|
Playing Now