Home
Class 10
MATHS
side AB and AC and median AD od a triang...

side AB and AC and median AD od a triangle ABC are respectively proportional to side PQ and PR and median PM of another triangle PQR. Show that `DeltaABC~DeltaPQR`

Answer

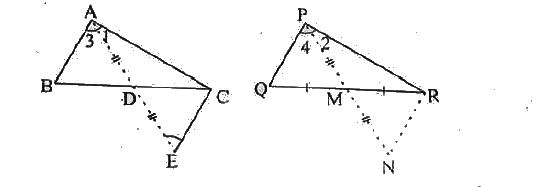
Step by step text solution for side AB and AC and median AD od a triangle ABC are respectively proportional to side PQ and PR and median PM of another triangle PQR. Show that DeltaABC~DeltaPQR by MATHS experts to help you in doubts & scoring excellent marks in Class 10 exams.

Doubtnut Promotions Banner Mobile Dark
|

Topper's Solved these Questions

  • TRIANGLES

    SUBHASH PUBLICATION|Exercise EXERCISE 2.4|7 Videos

  • TRIANGLES

    SUBHASH PUBLICATION|Exercise EXERCISE 2.4 (Tick the correct answer and justify) :|2 Videos

  • TRIANGLES

    SUBHASH PUBLICATION|Exercise EXERCISE 2.2|12 Videos

  • SURFACE AREAS AND VOLUMES

    SUBHASH PUBLICATION|Exercise EXERCISE 15.5|4 Videos

Similar Questions

Explore conceptually related problems

sides AB and BC and median AD of a triangle ABC are respectively proportional to side PQ and QR median PM of DeltaPQR (see Fig ). Show that DeltaABC~DeltaPQR

Two sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of Delta PQR. Show that Delta ABM ~= Delta PQN (ii) Delta ABC ~= Delta PQR

S and T are points on sides PR and QR of Delta PQR such that . Show that Delta RPQ~Delta RTS .

The median AD of the triangle ABC is bisected at E and BE meets AC at F. Find AF:FC.

In the Given figure, E is any point on median AD of a triangle ABC Show that ar (ABE) = ar (ACE)

S and T are point on sides PR and QR of Delta PQR such that /_ P = /_ RTS . Show that Delta RPQ - Delta RTS .

The sides AB and AC and the perimeter P_(1) of DeltaABC are respectively three times the corresponding sides DE and DF and the perimeter P_(2) of DeltaDEF . Are the two triangles similar? If yes, find (ar(DeltaABC))/(ar(DeltaDEF)) .

D, E and F are respectively the mid-points of sides AB, BC and CA of Delta ABC . Find the ratio of the areas of Delta DEF and Delta ABC .

In the given figure, AB||DC and AD||BC show that DeltaABC ~= Delta CDA .

E and F are respectively the mid-points of equal sides AB and AC of DeltaABC (see figure) Show that BF = CE.

Home
Profile