Home
Class 9
MATHS
In Fig , sides QP and RQ and RQ of Delta...

In Fig , sides QP and RQ and RQ of `DeltaPQR` are produced to points S and T respectively . If `lfloorSRP = 135^(@) and lfloorPQT=110^(@) , " find " lfloorPRO`.

Text Solution

Verified by Experts

The correct Answer is:
`65^(@)`
Promotional Banner

Topper's Solved these Questions

  • LINES AND ANGLES

    SUBHASH PUBLICATION|Exercise EXERCISE 3.2|3 Videos

  • LINEAR EQUATIONS IN TWO VARIABLES

    SUBHASH PUBLICATION|Exercise EXERCISE 10.4|4 Videos

  • NUMBER SYSTEM

    SUBHASH PUBLICATION|Exercise Exercise 1.6|11 Videos

Similar Questions

Explore conceptually related problems

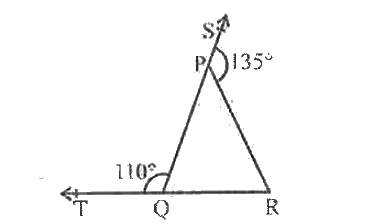
In the given figure sides QP and RQ of ΔPQR are produced to points S and T respectively. If angleSPR = 135^(@) and anglePQT = 110^(@) , find anglePRQ.

In Fig , the side QR and DeltaPQR is produced to a point S. If the bisector of lfloorPQR and lfloorPRS meet at point T the prove that lfloor QTR=(1)/(2) lfloorQPR.

Let AP and BQ be two vertical poles at points A and B, respectively. If AP = 16 m, BQ = 22 m and AB = 20 m, then find the distance of a point R on AB from the point A such that RP^(2) + RQ^(2) is minimum.

S and T are points on sides PR and QR of DeltaPQR such that angleP = angleRTS . Show that DeltaRPQ ~DeltaRTS .

In fig, arcs are drawn by taking vertices A, B and C of an equilateral triangle of side 10 cm, to intersect the sides BC, CA and AB at their respective mid-points D, E and F. Find the area of the shaded region. ("Use " pi = 3.14) .

Find the value of lamda so that the points P, Q, R and S on the sides OA, OB, OC and AB, respectively, of a regular tetrahedron OABC are coplanar. It is given that (OP)/(OA) = (1)/(3), (OQ)/(OB) = (1)/(2), (OR)/(OC) = (1)/(3) and (OS)/(AB)= lamda .