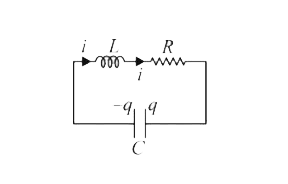
Recommended Questions
- A LCR circuit behaves like a damped harmonic oscillator. Comparing it ...
03:12
|
Playing Now - There is a LCR circuit , If it is compared with a damped oscillation o...
03:32
|
Play - In a damped harmonic oscillator, periodic oscillations have ………. ampli...
03:29
|
Play - A LCR circuit behaves like a damped harmonic oscillator. Comparing it ...
03:12
|
Play - An LCR circuit behaves like a damped harmonic oscillator. Comparing it...
04:13
|
Play - An LCR series circuit behaves like a damped harmonic oscillator. Compa...
04:53
|
Play - For a damped oscillation of a particle, show that time taken for the a...
04:28
|
Play - A LCR circuit behaves like a damped harmonic oscillator. Comparing it ...
03:41
|
Play - There is a LCR circuit , If it is compared with a damped oscillation o...
05:52
|
Play