A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
SIMPLE HARONIC MOTION
MOTION|Exercise EXERCISE -1 ( SECTION-D ) ( Combination of springs)|3 VideosSIMPLE HARONIC MOTION
MOTION|Exercise EXERCISE -1 ( SECTION-E,F ) ( – Angu lar shm & s implependulum)|10 VideosSIMPLE HARONIC MOTION
MOTION|Exercise EXERCISE -1 ( SECTION-B ) (Time per iod and angu larfrequency in SHM)|8 VideosSIMPLE HARMONIC MOTION
MOTION|Exercise EXERCISE -3 Section - B Previous Year Problems | JEE MAIN|23 VideosSOUND WAVES
MOTION|Exercise Exercise - 3 (Section - B)|14 Videos
Similar Questions
Explore conceptually related problems
MOTION-SIMPLE HARONIC MOTION -EXERCISE -1 ( SECTION-C ) ( Two block system)
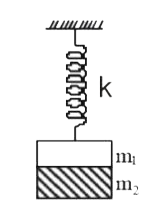
- Two masses m(1) and m(2) are suspended together by a massless spring o...
Text Solution
|
- A block of mass m =1 kg placed on top of another block of mass M = 5 k...
Text Solution
|
- A block of mass m moves with a speed v towards the right block which i...
Text Solution
|
- Two blocks each of mass m are connected with springs each of force con...
Text Solution
|
- A block P of mass m is placed on horizontal frictionless plane. A seco...
Text Solution
|
- Four springs of constant as shown are attached to a pair of masses m e...
Text Solution
|