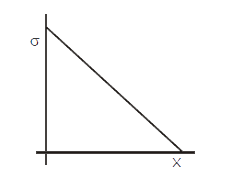
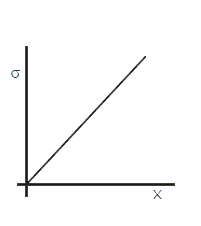
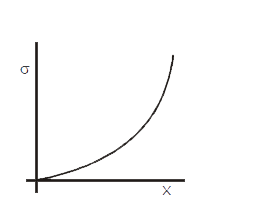
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
ELASTICITY AND THERMAL EXPANSION
MOTION|Exercise Exercise - 2 (Level-I) (Section C - Youngs Modulus, Poissions Ratio)|2 VideosELASTICITY AND THERMAL EXPANSION
MOTION|Exercise Exercise - 2 (Level-I) (Section D - Thermal Expansion (Solid , Liquids & Gas) & types, Applications (Ex Bimetallic strip etc))|2 VideosELASTICITY AND THERMAL EXPANSION
MOTION|Exercise Exercise - 2 (Level-I) (Section A - Stress & types, Strain & types + Types of Modulus + Energy Problems + Graphs)|3 VideosELASTICITY
MOTION|Exercise EXERCISE -3|60 VideosElectrical Instrument
MOTION|Exercise EXERCISE -3|16 Videos