Text Solution
Verified by Experts
|
Topper's Solved these Questions
CURRENT ELECTRICITY
NCERT|Exercise EXERCISE|23 VideosView PlaylistATOMS
NCERT|Exercise Exercise|17 VideosView PlaylistDUAL NATURE OF RADIATION AND MATTER
NCERT|Exercise Exercise|37 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
NCERT-CURRENT ELECTRICITY-EXERCISE
- Battery of 10 V and negligible internal resistance is connected across...
08:00
|
Playing Now - The storage battery of a car has an emf of 12 V. If the internal resis...
01:16
|
Play - A battery of emf 10 V and internal resistance 3 Omega is connected to...
01:42
|
Play - (a) Three resistors 1 Omega, 2Omega and 3 Omega are combined in series...
01:40
|
Play - (a) Three resistors 2 Omega, 4 Omega and 5 Omega are combined in paral...
02:56
|
Play - At room temperature (27.0^@C) the resistance of a heating element is 1...
02:06
|
Play - A negligibly small current is passed through a wire of length 15 m and...
01:10
|
Play - A silver wire has a resistance of 2.1 Omega at 27.5^@C, and a resistan...
02:02
|
Play - A heating element using nichrome connected to a 230 V supply draws an ...
04:05
|
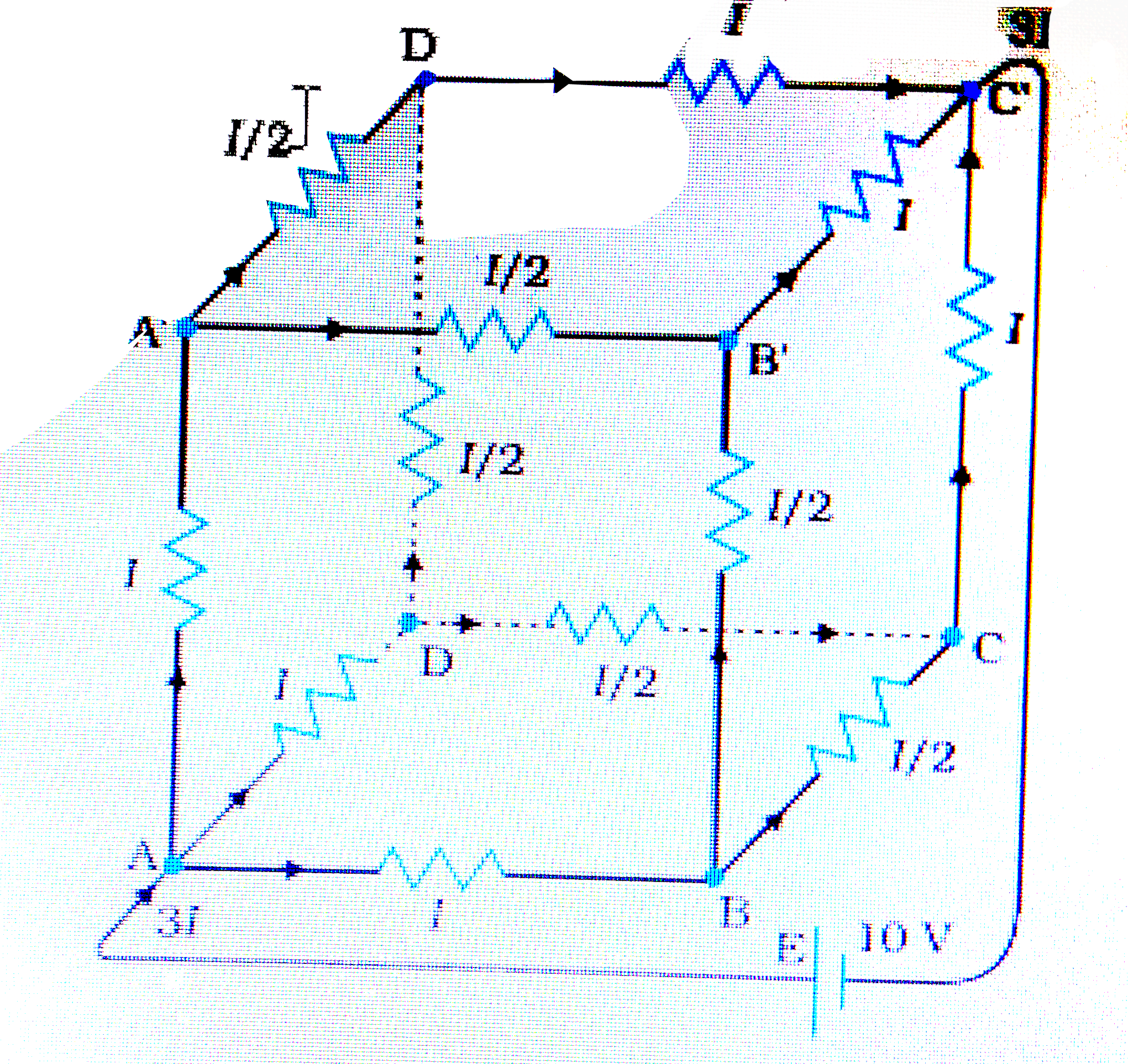
Play - Determine the current in each branch of the network shown in fig.
06:04
|
Play - (i) In a metre bridge, the balance point is found to be at 39.5 cm fro...
04:06
|
Play - A storage battery of emf 8.0 V and internal resistance 0.5 Omega is be...
06:06
|
Play - In a potentiometer arrangement, a cell of emf 1.25 V gives a balance p...
04:21
|
Play - The number density of free electrons in a copper conductor is estimate...
02:14
|
Play - The earth's surface has a negative surface charge density of 10^(-9) C...
03:31
|
Play - (a) Six lead-acid type of secondary cells each of emf 2.0 V and intern...
05:20
|
Play - Two wires of equal length, one of aluminium and the other of copper ha...
03:02
|
Play - What conclusion can you draw from the following observations on a resi...
01:12
|
Play - Answer the following questions : (a) A steady current flows in a metal...
04:32
|
Play - Choose the correct alternatives : (a) Alloys of metals usually have...
04:56
|
Play - (a) Given n resistors each of resistance R. How will you combine them ...
02:48
|
Play