Text Solution
Verified by Experts
|
Topper's Solved these Questions
CENTRE OF MASS
MOTION|Exercise Exercise - 1|71 VideosView PlaylistCENTRE OF MASS
MOTION|Exercise Exercise - 2 (Level-I)|40 VideosView PlaylistCapacitance
MOTION|Exercise EXERCISE -4 LEVEL II|19 VideosView PlaylistCIRCULAR MOTION
MOTION|Exercise EXERCISE - 4|16 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
MOTION-CENTRE OF MASS-Exercise - 4 Level-II
- On a frictionless surface, a ball of mass m moving at a speed v makes ...
05:16
|
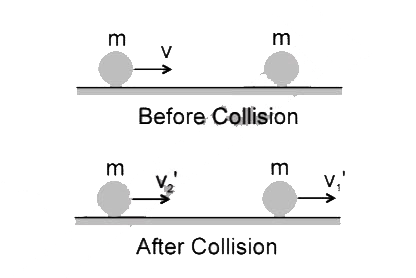
Playing Now - STATEMENT-l : In an elastic collision between two bodies, the relative...
03:58
|
Play - A particle moves in the X-Y plane under the influence of a force such ...
02:55
|
Play - Two balls having linear momenta vecp(1)=phati and vecp(2)=-phati, und...
02:02
|
Play - A small block of mass M moves on a frictionless surface of an incline...
04:27
|
Play - A small block of mass M moves on a frictionless surface of an incline...
04:27
|
Play - A small block of mass M moves on a frictionless surface of an incline...
04:27
|
Play - If the resultant of all the external forces acting on a system of part...
04:52
|
Play - Look at the drawing given in the figure which has been drawn with ink ...
01:36
|
Play - Two small particles of equal masses stant moving in opposite directio...
06:06
|
Play - There object A ,B and C are kept is a straing line a fritionlas horize...
07:42
|
Play - A point mass of 1 kg collides elastically with a stationary point mass...
03:25
|
Play - A ball of mass 0.2 kg rests on a vertical post of height 5 m. A bullet...
05:58
|
Play - A particle of mass m is projected from the ground with an initial spee...
06:19
|
Play - A pulse of light of duration 100ns is absorbed completely by a small o...
01:55
|
Play - A tennis ball dropped on a barizoontal smooth surface , it because bac...
04:20
|
Play - A block of mass M has a circular cut with a frictionless surface as sh...
07:50
|
Play - A flat plate is moving normal to its plane through a gas under the act...
Text Solution
|
Play - Consider regular polygons with number of sides n = 3, 4, 5 ...... as s...
04:56
|
Play - A spring-block system is resting on a frictionless floor as shown in t...
09:23
|
Play - A small particle of mass m moving inside a heavy, hollow and straight ...
06:24
|
Play