Home
Class 12
PHYSICS
When two soap bubbles of radius r(1) " a...

When two soap bubbles of radius `r_(1) " and " r_(2)(r_(2) gt r_(1))` coalesce, the radius of curvature of common surface is

Text Solution

Verified by Experts

`:'r_(1)ltr_(2)`
`:.P_(1)gtR_(2)` Small portion of bubbles is in contact and in equilibrium

`P_(1)-P_(2)=(4T)/(r)implies(4T)/(r_(1))-(4T)/(r_(2))impliesr=(r_(1)r_(2))/(r_(2)-r_(1))`
Promotional Banner

Topper's Solved these Questions

  • SURFACE TENSION

    MOTION|Exercise Exercise - 1 Objective Problems | NEET|47 Videos

  • SURFACE TENSION

    MOTION|Exercise Exercise - 2 Objective Problems | NEET|28 Videos

  • SURFACE TENSION

    MOTION|Exercise Exercise - 3 | Section - B Previous Year Problems | AIEEE|12 Videos

  • SOUND WAVES

    MOTION|Exercise Exercise - 3 (Section - B)|14 Videos

  • SURFACE TENSION & VISCOSITY

    MOTION|Exercise Exercise - 4 | Level-II Previous Year | JEE Advanced|12 Videos

Similar Questions

Explore conceptually related problems

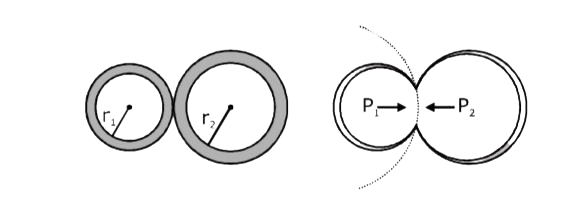
When two soap bubbles of radii a and b ( b gt a ) coalesce, the radius of curvature of common surface is :

Two soap bubbles of radius r_(1) and r_(2) combine. Find radius of curvature of the common surface separating them.

Two soap bubbles of radii r_(1) and r_(2) are attached as shown. Find the radius of curvature of the common film ACB.

Prove that if two bubbles of radii r_(1) and r_(2)(r_(1)ltr_(2)) come in contact with each other then the radius of curvature of the common surface r=(r_(1)r_(2))/(r_(2)-r_(1))

Two soap bubbles each of radius r are touching each other. The radius of curvature of the common surface will be:

Under isothermal condition two soap bubbles of radii r_(1) and r_(2) coalesce to form a single bubble of radius r. The external pressure is p_(0) . Find the surface tension of the soap in terms of the given parameters.

Two soap bubble of radius 2r and 3r are in contact with each other. If the radius of curvature of the interface between the bubble in nr then find the value of n :

If two bubble of radii 0.03 cm and 0.04 cm come in contact with each other then the radius of curvature of the common surface 'r' is given by.

A soap bubble of radius r_(1) is placed on another soap bubble of radius r_(2)(r_(1) lt r_(2)) . The radius R of the soapy film separating the two bubbles is :

If two soap bubbles of equal radii r coalesce then the radius of curvature of interface between two bubbles will be