Home
Class 12
MATHS
The curvey y=f(x) which satisfies the co...

The curvey y=f(x) which satisfies the condition `f'(x)gt0andf''(x)lt0`m for all real x, is

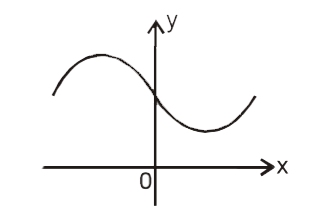
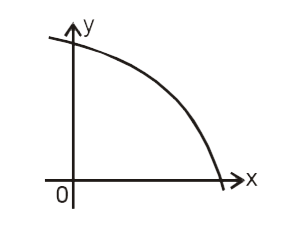
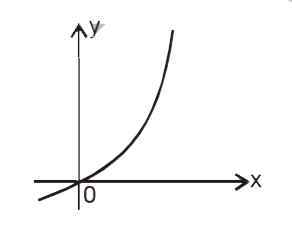
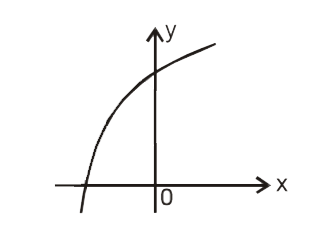
A

B

C

D

Text Solution

Verified by Experts

The correct Answer is:
D
Doubtnut Promotions Banner Mobile Dark
|

Topper's Solved these Questions

  • MONOTONOCITY

    MOTION|Exercise Exercise - 2 (Level-I) ( Objective Problems ) ( FINDING INTERVALS OF MONOTONOCITY )|2 Videos

  • MONOTONOCITY

    MOTION|Exercise Exercise - 2 (Level-I) ( Objective Problems ) ( FINDING VALUE OF VARIABLE GIVEN MONOTONIC BEHAVIOUR)|3 Videos

  • MONOTONOCITY

    MOTION|Exercise Exercise - 1 ( Objective Problems ) (SECTION-G : BASED ON LMVT)|6 Videos

  • METHOD OF DIFFERENTIATION

    MOTION|Exercise EXERCISE - 4 LEVEL -II|5 Videos

  • PARABOLA

    MOTION|Exercise EXERCISE - IV|33 Videos

Similar Questions

Explore conceptually related problems

Let f(x) be a function satisfying the condition f(-x)=f(x) for all real x.If f'(0) exists, then its value is equal to

A polynomial function f(x) satisfies the condition f(x)f((1)/(x))=f(x)+f((1)/(x)) for all x in R,x!=0. If f(3)=-26, then f(4)=

Knowledge Check

  • Let f'(x) gt0 and g'(x) lt 0 " for all " x in R Then

    A
    `f{g(x)gtf(g(X+1)}`
    B
    `f{g(x)gtf(g(X-1)}`
    C
    `g{f(x)gtg(f(X+1)}`
    D
    `g{f(x)gtg(f(X-1)}`

  • If f:RtoR is a function which satisfies the condition f(x)+f(y)=f((x+y)/(1+xy)) for all x, y in R except xy=-1 , then range of f(x) is

    A
    `[0,infty)`
    B
    `{0,1}`
    C
    `R`
    D
    `{0}`

  • A continuous and differentiable function f satisfies the condition, int_(0)^(x)f(t)dt=f^(2)(x)-1 for all real x. Then

    A
    f is monotonic increasing `AA x in R`
    B
    f is monotonic decreasing `AA x in R`
    C
    f is non monotonic
    D
    the graph of `y=f(x)` is a straight line

    • Similar Questions

    Explore conceptually related problems

    Suppose a differntiable function f(x) satisfies the identity f(x+y)=f(x)+f(y)+xy^(2)+xy for all real x and y .If lim_(x rarr0)(f(x))/(x)=1 then f'(3) is equal to

    Let f(x) be a differentiable function which satisfies the equation f(xy)=f(x)+f(y) for all x>0,y>0 then f'(x) equals to

    Let f(x) be a quadratic expression which is positive for all real x and g(x)=f(x)+f'(x)+f''(x) .A quadratic expression f(x) has same sign as that coefficient of x^2 for all real x if and only if the roots of the corresponding equation f(x)=0 are imaginary. For function f(x) and g(x) which of the following is true (A) f(x)g(x)gt0 for all real x (B) f(x)g(x)lt0 for all real x (C) f(x)g(x)=0 for some real x (D) f(x)g(x)=0 for all real x

    If a real valued function f(x) satisfies the equation f(x+y)=f(x)+f(y) for all x,y in R then f(x) is

    Let f(x) be a function which satisfy the equation f(xy)=f(x)+f(y) for all xgt0,ygt0 such that f'(1)=2 . Find the area of the region bounded by the curves y=f(x),y=|x^3-6x^2+11x-6| and x=0 .

    Home
    Profile