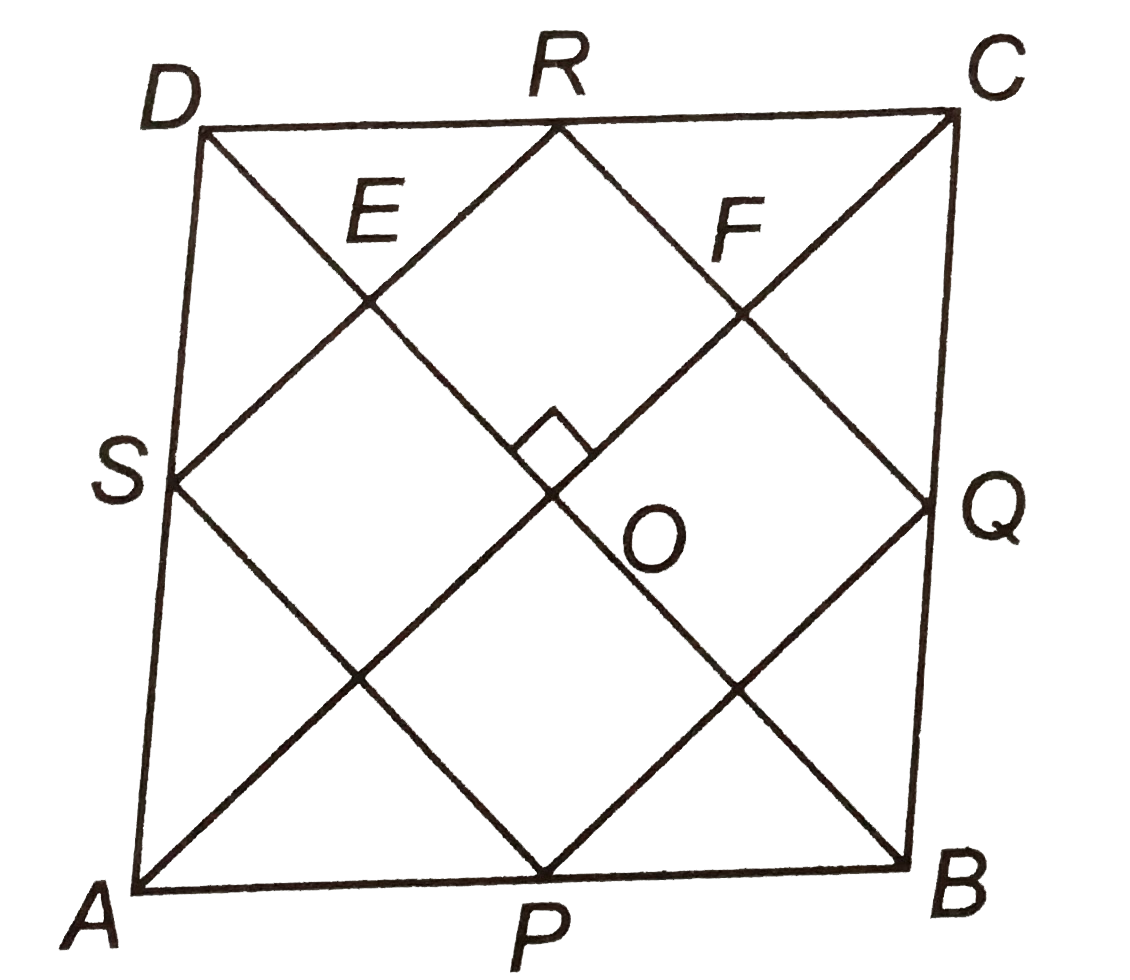
Text Solution
Verified by Experts
|
Topper's Solved these Questions
POLYNOMIALS
NCERT EXEMPLAR|Exercise Polynomials|72 VideosView PlaylistSTATISTICS AND PROBABILITY
NCERT EXEMPLAR|Exercise LONG ANSWER TYPE QUESTIONS|5 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
NCERT EXEMPLAR-QUADRILATERALS -Quadrilaterals
- Points P and Q have been taken on opposite sides AB and CD, respective...
02:43
|
Play - In figure, P is the mid-point of side BC of a parallelogram ABCD such ...
04:06
|
Play - A square is incribed in an isoceles right triangle, so that the square...
03:33
|
Play - In a parallelogram ABCD, AB = 10 cm and AD = 6 cm. The bisector of ang...
04:53
|
Play - P, Q , R and S are respectively the mid-points of the sides AB, BC, C...
05:07
|
Play - ABCD is a rhombus and P, Q, R and S are wthe mid-points of the sides A...
04:22
|
Play - P, Q, R and S are respectively the mid-points of sides AB, BC, CD and ...
05:41
|
Playing Now - If diagonal of a parallelogram bisects one of the angles of the parall...
04:41
|
Play - ABCD is a parallelogram in which P and Q are mid-points of opposite...
04:33
|
Play - ABCD is a quadrilateral in which AB||DC and AD = BC. Prove that angleA...
04:23
|
Play - In figure, AB||DE, AB=DE, AC||DF and AC=DF. Prove that BC||EF and BC=E...
04:16
|
Play - In A B C ,A D is the median through A and E is the mid-point of A D. ...
07:37
|
Play - The quadrilateral, formed by joining the mid-points of the sides of a ...
05:31
|
Play - In Figure, A B C D isa trapezium in which side A B is a parallel to si...
03:00
|
Play - The quadrilateral formed by the bisectors of the angles of a parallelo...
03:47
|
Play - P and Q are points on opposite sides AD and BC of a parallelogram ABCD...
02:17
|
Play - ABCD is a rectangle in which diagonal BD bisects angle B. then ABCD is...
02:50
|
Play - In DeltaA B C, D, E and F are respectively the mid-points of sides AB...
04:52
|
Play - Prove that the line segment joining the mid-points of the diagonals of...
04:23
|
Play - P is the mid-point of the side CD of a parallelogram ABCD. A line thro...
04:39
|
Play