Text Solution
Verified by Experts
Topper's Solved these Questions
ELECTROSTATICS
MOTION|Exercise SELF PRACTICE PROBLEM|27 VideosELECTROSTATICS
MOTION|Exercise Exercise -1 (Objective Problems | NEET)|105 VideosELECTROSTATICS
MOTION|Exercise Exercise -3 Section (B) Previous Year Problems | JEE Main|30 VideosELECTRONICS - SEMI CONDUCTOR
MOTION|Exercise EXERCISE - 3|29 VideosELECTROSTATICS - I
MOTION|Exercise EXERCISE - 4 (Level -II) PREVIOUS YEAR - JEE ADVANCED|13 Videos
Similar Questions
Explore conceptually related problems
MOTION-ELECTROSTATICS-SELF MISCELLANEOUS PROBLEM (Example )
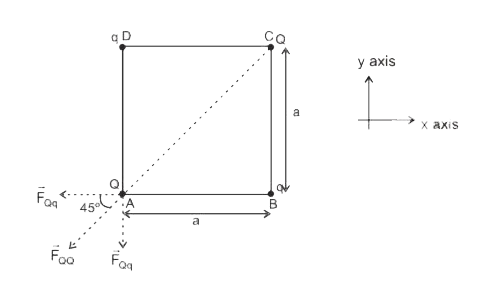
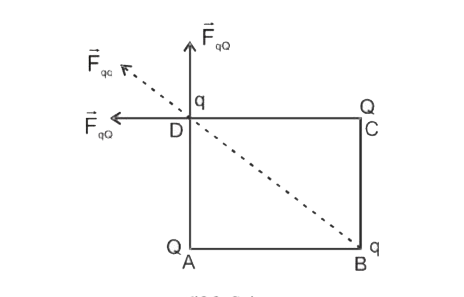
- A charges Q is placed at each of the two opposite corners of a square....
Text Solution
|
- Figure shows a uniformly charged thin non-conducting sphere of total c...
Text Solution
|
- Figure shows two concentric spheres of radii R(1) and R(2) (R(2) gt R(...
Text Solution
|
- Three identical spheres, each having a charge q and radius R. are kept...
Text Solution
|
- A Uniform electric field of 10NC ^(-1) exists in the vertically downwa...
Text Solution
|
- An electric field of 20 N//C exists along the x-axis in space. Calcula...
Text Solution
|
- A point charge of charge -q and mass m is released with negligible spe...
Text Solution
|
- Four small point charges (each of equal magnitude q) are placed at fou...
Text Solution
|
- If V=x^(2)y+y^(2)z then find vec(E) at (x, y, z)
Text Solution
|
- If E=2r^(2) then find V(r)
Text Solution
|
- A charge Q is uniformly distributed over a rod of length l. Consider a...
Text Solution
|
- A charge Q is placed at the centre of a cube. Find the flux of the ele...
Text Solution
|
- An isolated conducting sphere of charge Q and radius R is grounded by ...
Text Solution
|
- Two uncharged and parallel conducting sheets, each of area A are place...
Text Solution
|
- A positive charge q is placed in front of a conducting solid cube at a...
Text Solution
|