A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
KVPY
KVPY PREVIOUS YEAR|Exercise PART-II MATHEMATICS|10 VideosView PlaylistKVPY
KVPY PREVIOUS YEAR|Exercise Part A - Mathematics|20 VideosView PlaylistKVPY
KVPY PREVIOUS YEAR|Exercise PART-2(MATHEMATICS)|10 VideosView PlaylistKVPY 2021
KVPY PREVIOUS YEAR|Exercise PART II MATHEMATICS|4 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
KVPY PREVIOUS YEAR-KVPY-PART -I MATHEMATICS
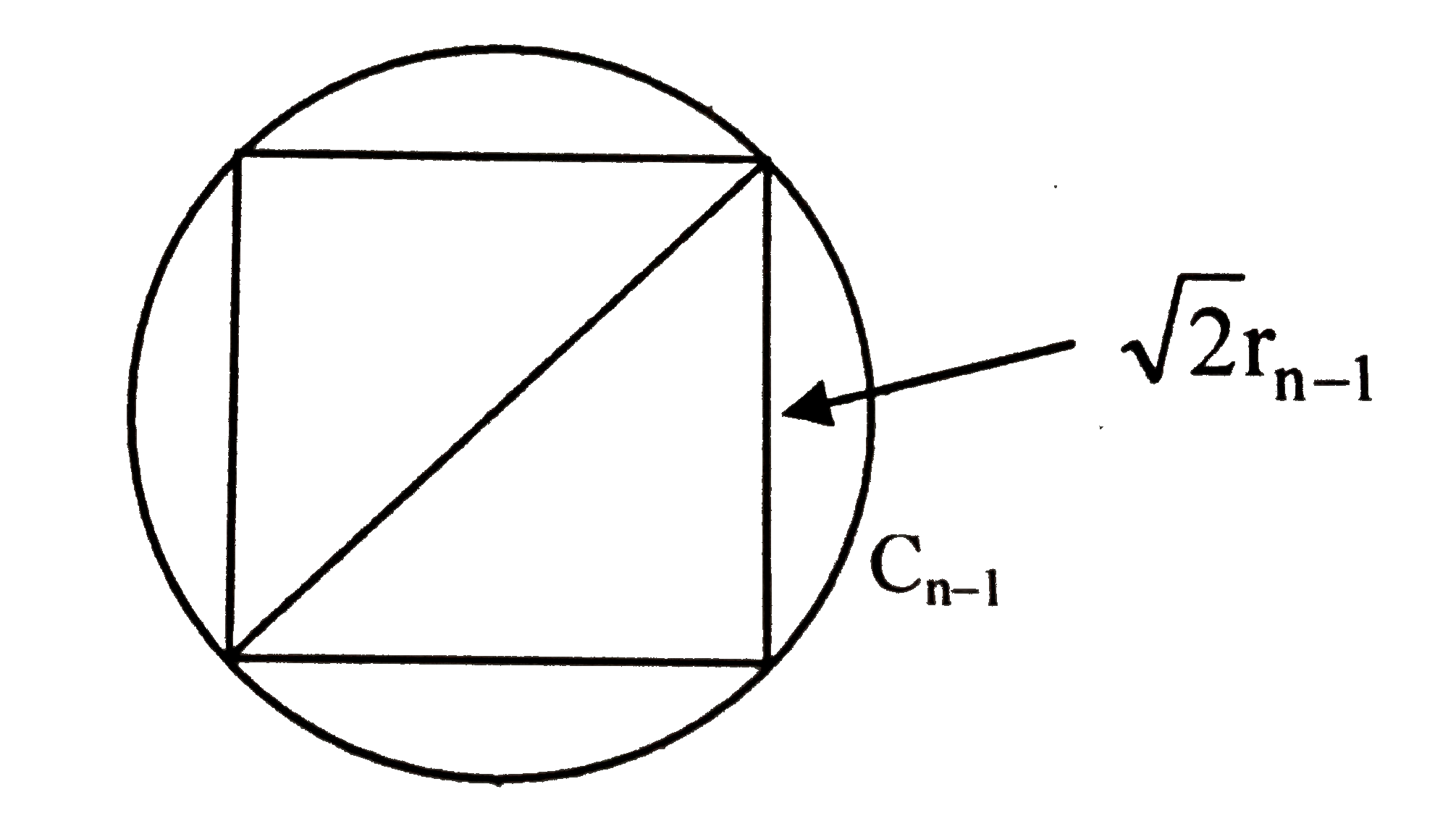
- Let C(0) be circle of radius 1. For nge1, let C(n) be a circle whose ...
03:30
|
Playing Now - For a real number r we denote by [r] the largest integer less than or ...
04:15
|
Play - For each positive integer n, let An=max{(C(n,r) 0 le r le n} then the ...
09:35
|
Play - Let b,dgt0 . The locus of all points P(r,theta) for which the line OP ...
02:30
|
Play - Let C be the circle x^(2)+y^(2)=1 in the xy-plane . For each tge0, let...
06:16
|
Play - In an ellipse, its foci and the ends of its major axis are equally spa...
02:53
|
Play - Let ABC be a triangle such that AB=BC. Let F be midpoint of AB and X...
05:57
|
Play - The number of solutions to the equations cos^(4)x+(1)/(cos^(2)x)=sin^...
05:16
|
Play - Consider the function f(x)= {{:((x+5)/(x-2),"if " xne 2),(" 1", "if "...
03:26
|
Play - For a real number x let [x] denote the largest number less than or equ...
03:45
|
Play - Let :[0,pi]rarrR be defined as f(x) ={{:(sinx,"if x is irrational a...
03:34
|
Play - Let f: [0,1]rarr[0,oo] be a continuous function such that int(0)^(1) f...
Text Solution
|
Play - A continuous function f: R rarrR satisfies the equation f(x)=x+int(0)^...
04:53
|
Play - For a real number x let [x] denote the largest integer les than or eq...
04:30
|
Play - Two persons A and B throw a (fair) die (six faced cube faces numbered ...
04:15
|
Play - Let nge3. A list of numbers x(1),x(2),....,x(n) has mean mu and standa...
Text Solution
|
Play - What is the angle substended by an edge of regular tetrahedron at its ...
Text Solution
|
Play - Let S={(a,b): a,binZ,0lea,ble18} . The number of elements (x ,y) in Su...
07:15
|
Play - For a real number r let [r] denote the largest integer less than or eq...
Text Solution
|
Play - Let X be a set of 5 elements. The number d of ordered pairs (A,B) of s...
Text Solution
|
Play