Home
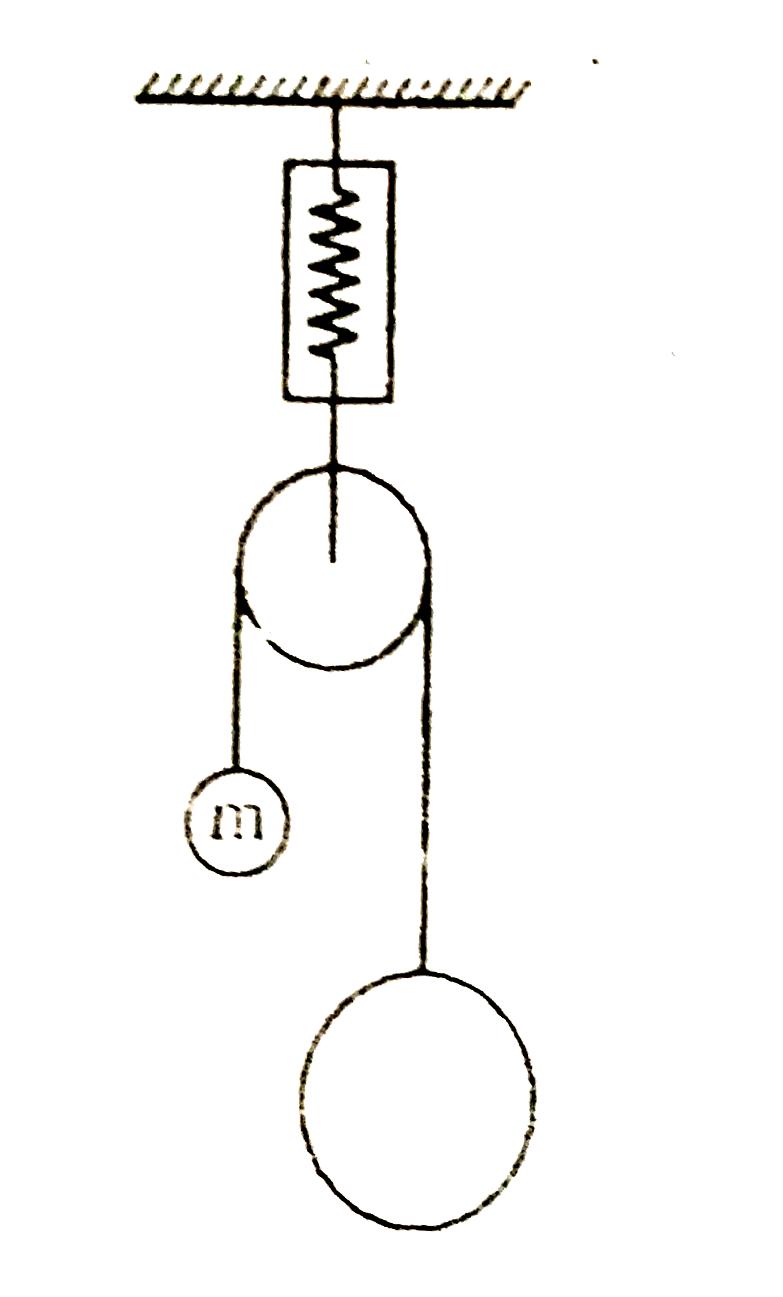
Class 12
PHYSICS
A light particle of mass m is connected ...

A light particle of mass m is connected to another very heavy particle by means of a light inextensible string that passes over a smooth pulley. The reading of the spring balance is approxinately

A

`4 mg`

B

`gt gt mg`

C

zero

D

`2 mg`

Text Solution

Verified by Experts

The correct Answer is:
A
`T = (2m_(1)m_(2)g)/(m_(1) + m_(2))`
`m_(1) = m`
`m_(2) =` very heavy mass (M)
`T = (2mg)/((m+ M)/(M))`
`T = (2mg)/(1 + (m)/(M))`
`T ~~ 2mg" " m lt lt M`
spring balance will measure
`2T = 2 xx 2mg = 4 mg`
Doubtnut Promotions Banner Mobile Dark
|

Topper's Solved these Questions

  • TEST PAPERS

    BANSAL|Exercise PHYSICS PART (A)|32 Videos

  • TEST PAPERS

    BANSAL|Exercise PHYSICS PART (B)|3 Videos

  • TEST PAPERS

    BANSAL|Exercise PHYSICS PART- C|4 Videos

  • SEMICONDUCTORS

    BANSAL|Exercise CBSE Question|32 Videos

Similar Questions

Explore conceptually related problems

A block of mass M is placed on a rough horizontal surface. It is connected by means of a light inextensible string passing over a smooth pulley . The other end of string is connected to a block of mass m. There is no friction between vertical surface and block m The minimum value of coefficient of friction mu such that system remains at rest , is

A block of mass M is placed on a rough horizontal surface. It is connected by means of a light inextensible string passing over a smooth pulley . The other end of string passing over a smooth pulley. The other end of string is connected to a block of mass m. There is no friction between vertical surface and block m If the whole system ( horizontal surface + blocks ) accelerates towards right the value of maximum on the horizontal surface is

Knowledge Check

  • A block of mass m_(1) lies on a smooth horizontal table and is connected to another freely hanging block of mass m_(2) by a light inextensible string passing over a smooth fixed pulley situated at the edge o fthe table. Initially the system is at rest with m_(1) a distance d from the pulley. Then the time taken for m_(1) to reach the pulley is.

    A
    `(m_(2)g)/(m_(1)+m_(2))`
    B
    `sqrt((2d(m_(1)+m_(2)))/(m_(2)g))`
    C
    `sqrt((2m_(2)d)/((m_(1)+m_(2))g)`
    D
    None of thess

  • Two masses of 10 kg and 6 kg connected at the two ends of an inextensible string pass over a smooth frictionless pulley . Calculate acceleration of the system and tension in the string .

    A
    71.5 N
    B
    72.5 N
    C
    73.5 N
    D
    74.5 N

  • In the figure shown, a particle of small mass m is joined to a very heavy mass M (M >> m) by a light string passing over a light pulley. The total downward force on the pulley by the string is :

    A
    mg
    B
    2 mg
    C
    4 mg
    D
    (M + m) g

    • Similar Questions

    Explore conceptually related problems

    Two particles having mass ratio n:1 are interconnected by a light inextensible string that passes over a smooth pulley . If the system is released , then the acceleration of the centre of mass of the system is

    Two particles A and B having equal mass are interconnected by a light inextensible string that passes over a smooth pulley. One of the amsses is pulled downward by a constant force 'F' as shown in diagram, then find the acceleration of the centre of mass of the system (A+B) .

    Two masses 8 kg and 12 kg are connected at the two ends of a light inextensible string that passes over a frictionless pulley Fibd the acceleration of the masses and tension in the string , when the masses are released .

    Two masses M and m are connected at the two ends of an inextensible string. The string passes over a smooth frictionless pulley. Calculate the acceleration of the masses and the tension in the string. Given Mgtm .

    A particle of small m is joined to a very heavy body by a light string passing over a light pulley. Both bodies are free to move. The total downward force on the pulley is

    Home
    Profile