A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
WORK, ENERGY AND POWER
FIITJEE|Exercise NUMERICAL BASED QUESTIONS|4 VideosView PlaylistWORK, ENERGY AND POWER
FIITJEE|Exercise MATRIX MATCH TYPE|6 VideosView PlaylistWORK, ENERGY AND POWER
FIITJEE|Exercise SOLVED PROBLEMS ( OBJECTIVE) ASSERTION REASONING TYPE|1 VideosView PlaylistTEST PAPERS
FIITJEE|Exercise PHYSICS|747 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
FIITJEE-WORK, ENERGY AND POWER -COMPREHENSIONS ( Comprehension-I)
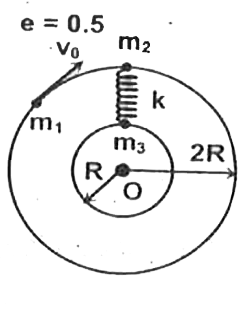
- Three particles each of mass 'm' can slide on fixed frictionless circu...
Text Solution
|
Playing Now - Three particles each of mass m can slide on fixed friction less circul...
07:12
|
Play - In a children\'s park, there is a slide which has a total length of 10...
04:09
|
Play - In a children\'s park, there is a slide which has a total length of 10...
04:09
|
Play - In a children\'s park, there is a slide which has a total length of 10...
04:09
|
Play - Newton's laws of motion are applicable in all inertial reference frame...
Text Solution
|
Play - Newton's laws of motion are applicable in all inertial reference frame...
Text Solution
|
Play