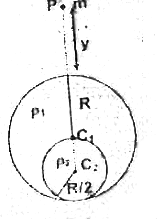Text Solution
Verified by Experts
Topper's Solved these Questions
GRAVITATION
FIITJEE|Exercise Assigment problems (Subjective) (level I)|14 VideosGRAVITATION
FIITJEE|Exercise Assigment problems (Subjective) (level II & III)|15 VideosGRAVITATION
FIITJEE|Exercise Matrix match type|2 VideosGMP ASSESMENT
FIITJEE|Exercise Numerical Based|61 VideosHEAT AND TEMPERATURE
FIITJEE|Exercise NUMERICAL BASES QUESTIONS|1 Videos
Similar Questions
Explore conceptually related problems
FIITJEE-GRAVITATION-Exercise
- On to a sphere of radius R//2 and density P(2) with centre at C(2) a s...
Text Solution
|
- A system consists of a thin ring of radius R and a very long uniform w...
Text Solution
|
- For given values of angular speed and acceleration due to gravity, fin...
Text Solution
|
- What is the gravitational potential energy of the earth and a satellit...
Text Solution
|
- At a point above the surface of the earth, the gravitational potential...
Text Solution
|
- Three identical point objects each of mass m are placed at the vertice...
Text Solution
|
- Find the gravitational potential due to a spherical shell of mass M a...
Text Solution
|
- The masses and radii of the earth an moon are M(1) and R(1) and M(2), ...
Text Solution
|
- A saturn year is 29.5 times the earth year. How far is the saturn from...
Text Solution
|
- Two hypothetical planets 1 and 2 are moving in the same eliptical path...
Text Solution
|
- A body is orbitting around the earth at mean radius 9 times as great a...
Text Solution
|