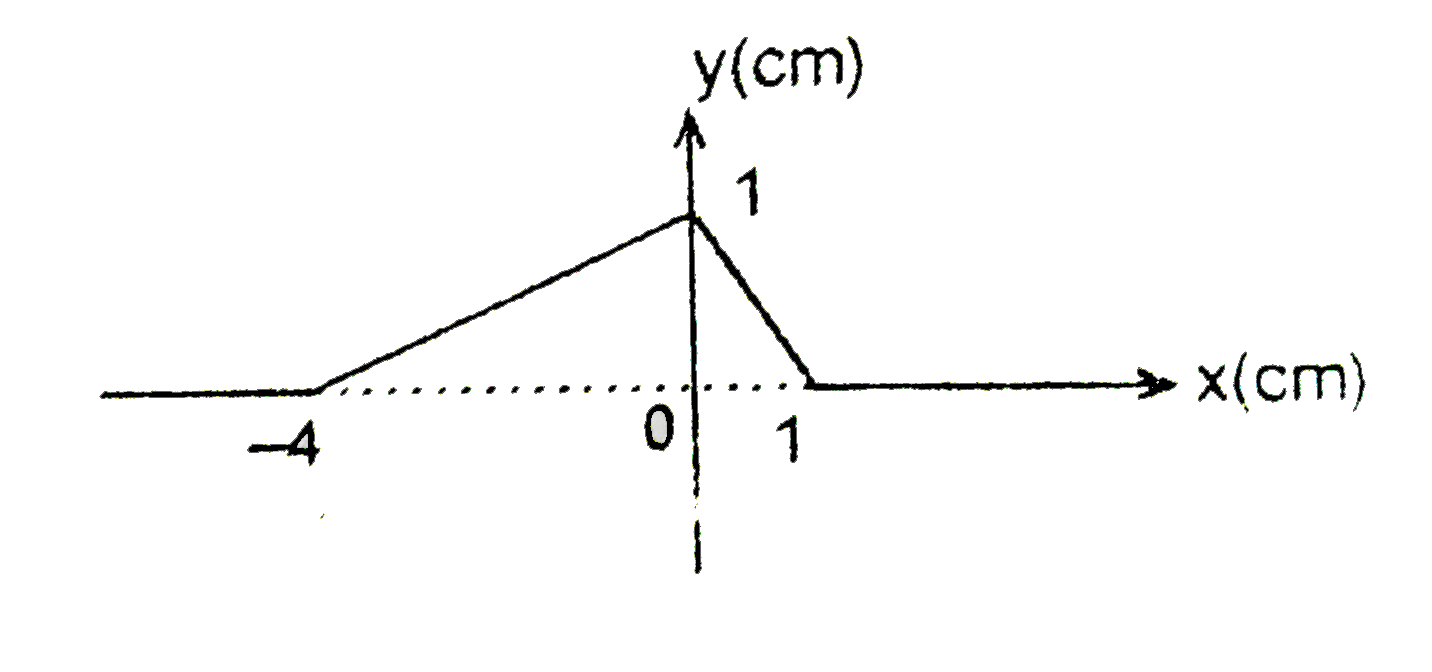
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
WAVE ON STRING
RESONANCE|Exercise Exercise- 3 PART II|7 VideosWAVE ON STRING
RESONANCE|Exercise Exercise- 3 PART I|19 VideosWAVE ON STRING
RESONANCE|Exercise Exercise- 2 PART III|15 VideosTRAVELLING WAVES
RESONANCE|Exercise Exercise- 3 PART II|7 VideosWAVE OPTICS
RESONANCE|Exercise Advanced Level Problems|8 Videos
Similar Questions
Explore conceptually related problems
RESONANCE-WAVE ON STRING -Exercise- 2 PART IV
- A pulse is started at a time t = 0 along the +x directions an a long, ...
Text Solution
|
- A pulse is started at a time t = 0 along the +x directions an a long, ...
Text Solution
|
- A pulse is started at a time t = 0 along the +x directions an a long, ...
Text Solution
|
- A transverse sinusoidal wave is generted at one end of long, horizonta...
Text Solution
|
- A transverse sinusoidal wave is generted at one end of long, horizonta...
Text Solution
|
- A transverse sinusoidal wave is generted at one end of long, horizonta...
Text Solution
|
- In the figure shown a sinusoidal wave is generated at the end 'A'. The...
Text Solution
|
- In the figure shown a sinusoidal wave is generated at the end 'A'. The...
Text Solution
|
- In the figure shown a sinusoidal wave is generated at the end 'A'. The...
Text Solution
|