Recommended Questions
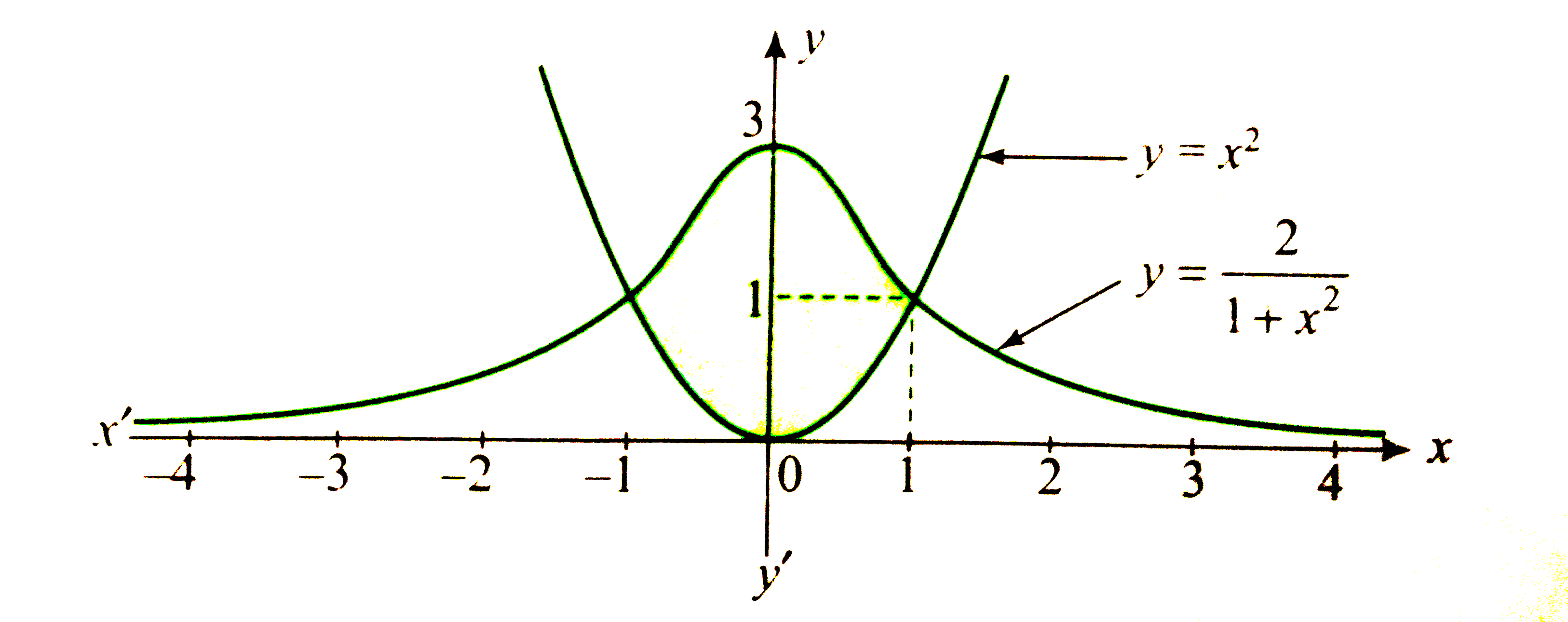
- Sketch the region bounded by the curves y=x^2a n dy=2/(1+x^2) . Find t...
06:10
|
Playing Now - Sketch the curves and identify the region bounded by the curves x=1...
05:57
|
Play - Sketch the region bounded by the curves y=x^2a n dy=2/(1+x^2) . Find t...
06:10
|
Play - Sketch the region bounded by the curves y=sqrt(5-x^2) and y=|x-1| and ...
07:39
|
Play - Sketch the curves and identity the region bounded by x=1/2,x=2,y=lnx ,...
07:55
|
Play - Sketch the region bounded by the curves y=sqrt(5-x^2) and y=|x-1| and ...
08:54
|
Play - Sketch the region bounded by the curves y=x^2a n dy=2/(1+x^2) . Find t...
03:29
|
Play - Sketch the curves and identify the region bounded by the curves x=1...
06:06
|
Play - Find the area bounded by the curves y=6x-x^2a n dy=x^2-2xdot
05:27
|
Play