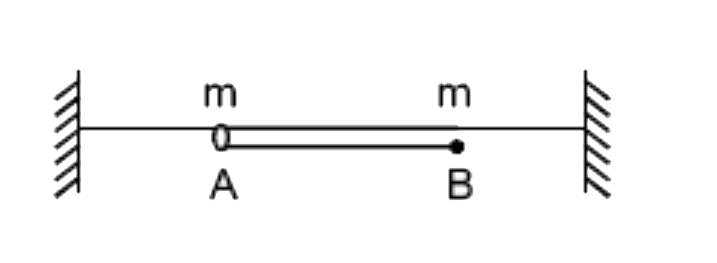
A small ring of mass m is constrained to...

A small ring of mass m is constrained to slide along a horizontal wire fixed between two rigid supports. The ring is connected to a particle of same mass by an ideal string & the whole system is released from rest as shown in the figure. If the coefficient of friction between ring A and wire is `(3)/(5)`, the ring will start sliding when the connecting string will make an angle `theta` with the vertical, then `theta` will be (particle is free to move and ring can slide only)

`30^(@)`

`45^(@)`

`60^(@)`

None of these

Text Solution

Verified by Experts

The correct Answer is:

Topper's Solved these Questions

NTA JEE MOCK TEST 106
NTA MOCK TESTS|Exercise PHYSICS|25 Videos
NTA JEE MOCK TEST 108
NTA MOCK TESTS|Exercise PHYSICS|25 Videos

Similar Questions

Explore conceptually related problems

A particle of mass m is rigidly attached at A to a ring of mass 3m and radius r . The system is released from rest and rolls without sliding. The angular acceleration of ring just after release is

A smooth ring of mass m can slide on a fixed horizontal rod. A string tied to the ring pases over a fixed pulley B and carries a block C of mass 2m as shown below. As the ring starts sliding

A ring of mass m can slide on the vertical smooth rod. Ring is connected by block with string as shown in figure. Pulley is of mass-less and smooth the system is released from reast. Initial tension in string is

A ring of mass M is kept on w horizontal rough surface . A force F is applied tangentially at its rim as shown . The coefficient of friction between the ring and surface is mu Then

A ring of mass m=10kg can slide through a vertical rod with friction. It is connected with a spring of force constant k=100Nm^-1 . The relaxed length of spring is 4m . The ring is displaced 3m as shown in the figure and released. Find velocity of ring when spring becomes horizontal.

A ring A which can slide on a smooth wire is connected to one end of a string as shown in fig. Other end of the string is connected to a hanging mass B. Find the speed of the ring when the string makes an angle theta with the wire and mass B is going down with a velocity v.

NTA MOCK TESTS-NTA JEE MOCK TEST 107-PHYSICS

A hollow charged metal sphere has radius r. If the potential differenc...
Text Solution
|
A sphere of radius 0.1m and mass 8 pi kg is attached to the lower en...
Text Solution
|
A small ring of mass m is constrained to slide along a horizontal wire...
Text Solution
|
Estimate the distance for which for which ray optics is good approxima...
Text Solution
|
A solid sphere of uniform density and radius R applies a gravitational...
Text Solution
|
A ball is projected from point A with velocity 10 ms^(-1) perpendicula...
Text Solution
|
If the series limit wavelength of the Lyman series of hydrogen atom is...
Text Solution
|
A tennis ball with (small) mass m(2) rests on the top of a basketball ...
Text Solution
|
The density of an electron-hole pair in a pure germanium is 3xx 10^(1...
Text Solution
|
The potnetial energy for a force field vecF is given by U(x, y)=cos(x+...
Text Solution
|
A long rigid wire lies along the X - axis and carries a current of 10 ...
Text Solution
|
A point object O is placed on the principal axis of a convex lens of f...
Text Solution
|
A block of the mass of 1 kg is moving on the x -axis. A force F acting...
Text Solution
|
The time period of oscillation of a simple pendulum is given by T=2pis...
Text Solution
|
Ice starts forming in lake with water at 0^(@)C and when the atmospher...
Text Solution
|
One mole of ideal gas goes through processP = (2V^2)/(1+V^2). Then ch...
Text Solution
|
The isotopic masses of .(1)^(2)H and .(2)^(4)He are 2.0141 and 4.0026 ...
Text Solution
|
A car is moving towards a high cliff. The car driver sounds a horn of ...
Text Solution
|
A storage battery of emf 8V and internal resistance is being charged...
Text Solution
|
A long solenoid of cross-sectional radius a has a thin insulates ...
Text Solution
|