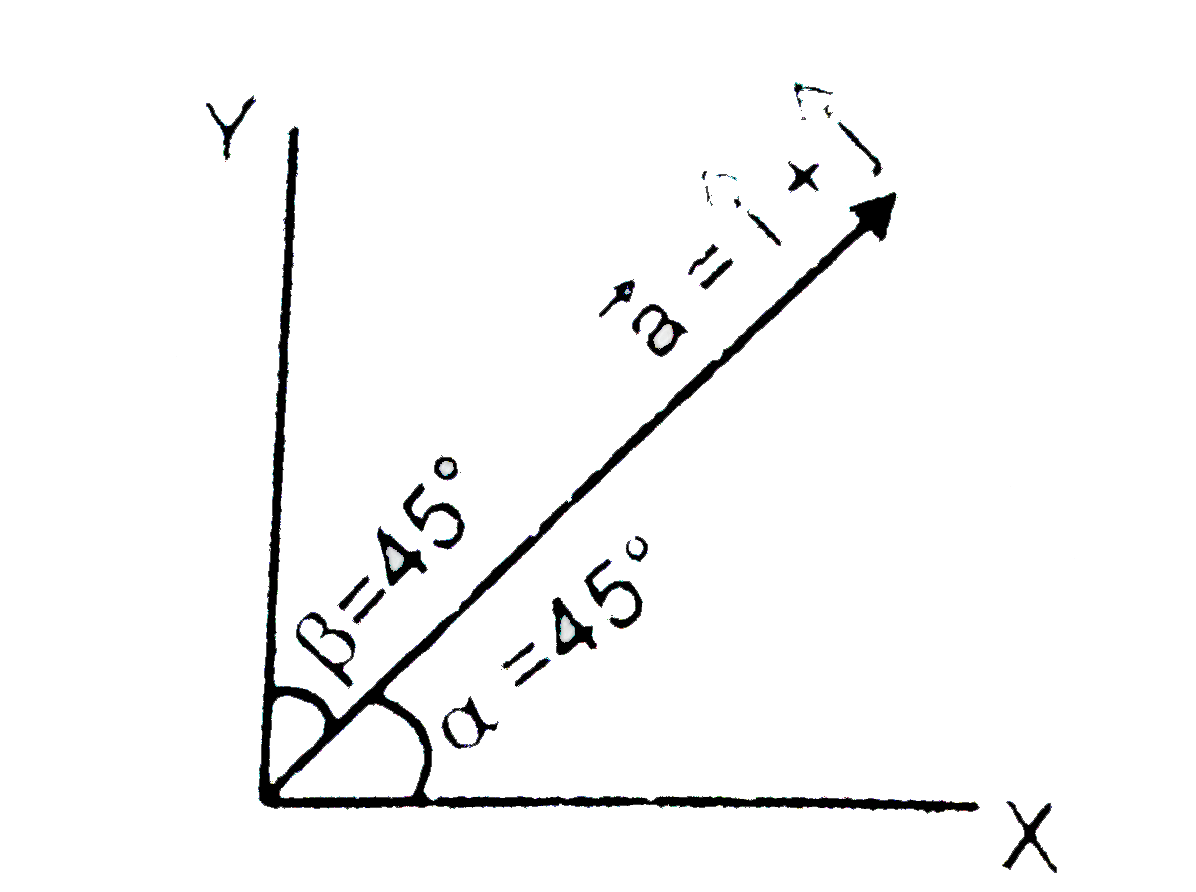Text Solution
Verified by Experts
|
Topper's Solved these Questions
BASIC MATHS
ALLEN|Exercise EXERCISE-1|128 VideosView PlaylistBASIC MATHS
ALLEN|Exercise EXERCISE-2|80 VideosView PlaylistAIIMS 2019
ALLEN|Exercise PHYSICS|40 VideosView PlaylistCIRCULAR MOTION
ALLEN|Exercise EXERCISE (J-A)|6 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems