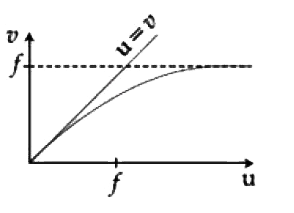
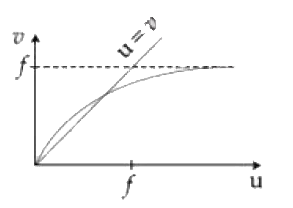
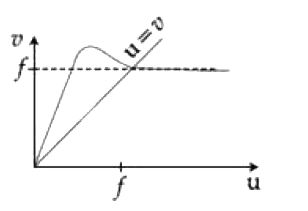
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
|
Topper's Solved these Questions
JEE MAINS
JEE MAINS PREVIOUS YEAR|Exercise Chemistry|1 VideosView PlaylistJEE MAINS 2021
JEE MAINS PREVIOUS YEAR|Exercise Physics (Section B )|10 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
JEE MAINS PREVIOUS YEAR-JEE MAINS 2020-PHYSICS
- A solid shere of radius R carries a charge Q distributed uniformly ov...
08:36
|
Play - A disc with moment of inertial I is rotating with some angular speed. ...
05:37
|
Play - For a concave lens of focal length f, the relation between object and ...
08:38
|
Playing Now - Three different process ses that can occur in an ideal monoatomic gas ...
02:05
|
Play - Number of molecules in a volumne of 4 cm^3 of a perfect monoatomic gas...
10:52
|
Play - A square loop of side 2a and carrying current I is kept in xz plane wi...
05:22
|
Play - A physical quantity z depends of four obserbles a, b, c and d, as z = ...
05:46
|
Play - A shell of relative density 27/9 w.r.t water is just submerged in wat...
04:51
|
Play - In a resonance tube experiment when the tube is filled with water up t...
05:09
|
Play - An electrical power line, having a total resistance of 2Omega, deliver...
02:30
|
Play - A bullet of mass 5 g travelling with a speed of 210 m/s, strikes a fix...
03:33
|
Play - A force vecF = (hati + 2hatj +3hatk)N acts at a point (4hati + 3hatj -...
02:57
|
Play - A beam of electrons of energy E scatters from a target having atomic s...
08:48
|
Play - A particle of mass 220 meV//c^2 collides with a hydrogen tom at rest. ...
04:22
|
Play - A compound microscope consists of an objective lens of focal length 1 ...
04:08
|
Play - Two concentric circular coils, C1 and C2, are ploced in the XY plane. ...
09:05
|
Play - A screw gauge has 50 divisions on its circular scale. The circular sca...
03:42
|
Play - A sound source S is moving along a straight track with speed v, and is...
07:16
|
Play - Fig, here shows P and Q as two equally intense coherent sources emitti...
08:16
|
Play - If the potential energy between two molecules is given by U= -(A)/(r^6...
03:18
|
Play