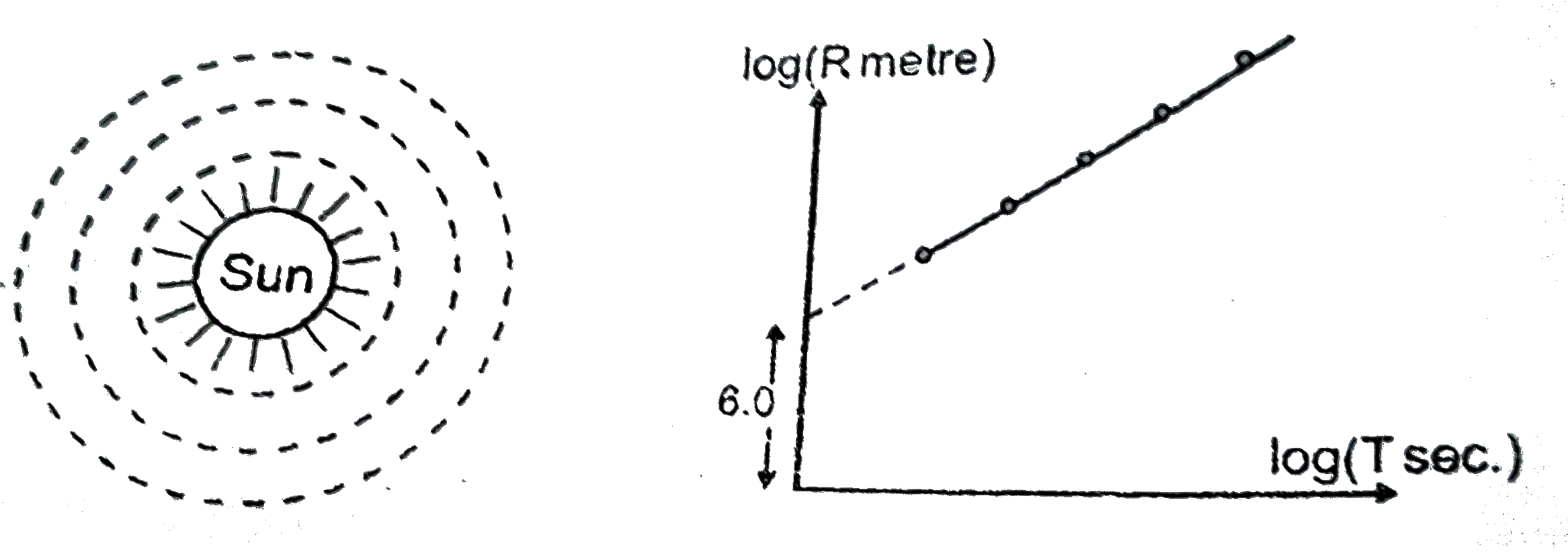
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
GRAVITATION
RESONANCE|Exercise EXERCISE-3 PART-1|15 VideosGRAVITATION
RESONANCE|Exercise EXERCISE-3 PART-2|11 VideosGRAVITATION
RESONANCE|Exercise EXERCISE-2 PART-3|12 VideosGEOMATRICAL OPTICS
RESONANCE|Exercise Advance level Problems|35 VideosNUCLEAR PHYSICS
RESONANCE|Exercise Advanced level solutions|16 Videos
Similar Questions
Explore conceptually related problems
RESONANCE-GRAVITATION-EXERCISE-2 PART-4
- Many planets are revolving around the fixed sun in circular orbits of ...
Text Solution
|
- Many planets are revolving around the fixed sun in circular orbits of ...
Text Solution
|
- Many planets are revolving around the fixed sun in circular orbits of ...
Text Solution
|
- An artificial satellite is moving in circular orbit around the earth w...
Text Solution
|
- An artificial satellite is moving in circular orbit around the earth w...
Text Solution
|
- An artificial satellite is moving in a circular orbit around the earth...
Text Solution
|
- A pair of stars rotates about their centre of mass One of the stars ha...
Text Solution
|
- A pair of stars rotates about their centre of mass One of the stars ha...
Text Solution
|
- A pair of stars rotates about their centre of mass One of the stars ha...
Text Solution
|