Text Solution
Verified by Experts
|
Topper's Solved these Questions
TEST PAPERS
BANSAL|Exercise PHYSICS PART (A)|32 VideosView PlaylistTEST PAPERS
BANSAL|Exercise PHYSICS PART (B)|3 VideosView PlaylistTEST PAPERS
BANSAL|Exercise PHYSICS PART- C|4 VideosView PlaylistSEMICONDUCTORS
BANSAL|Exercise CBSE Question|32 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
BANSAL-TEST PAPERS-PHYSICS
- A block of mass 2kg is sliding on a smooth surface. At t=0, its speed ...
04:01
|
Play - Under the condition shown in figure. Find out the minimum value of hor...
05:52
|
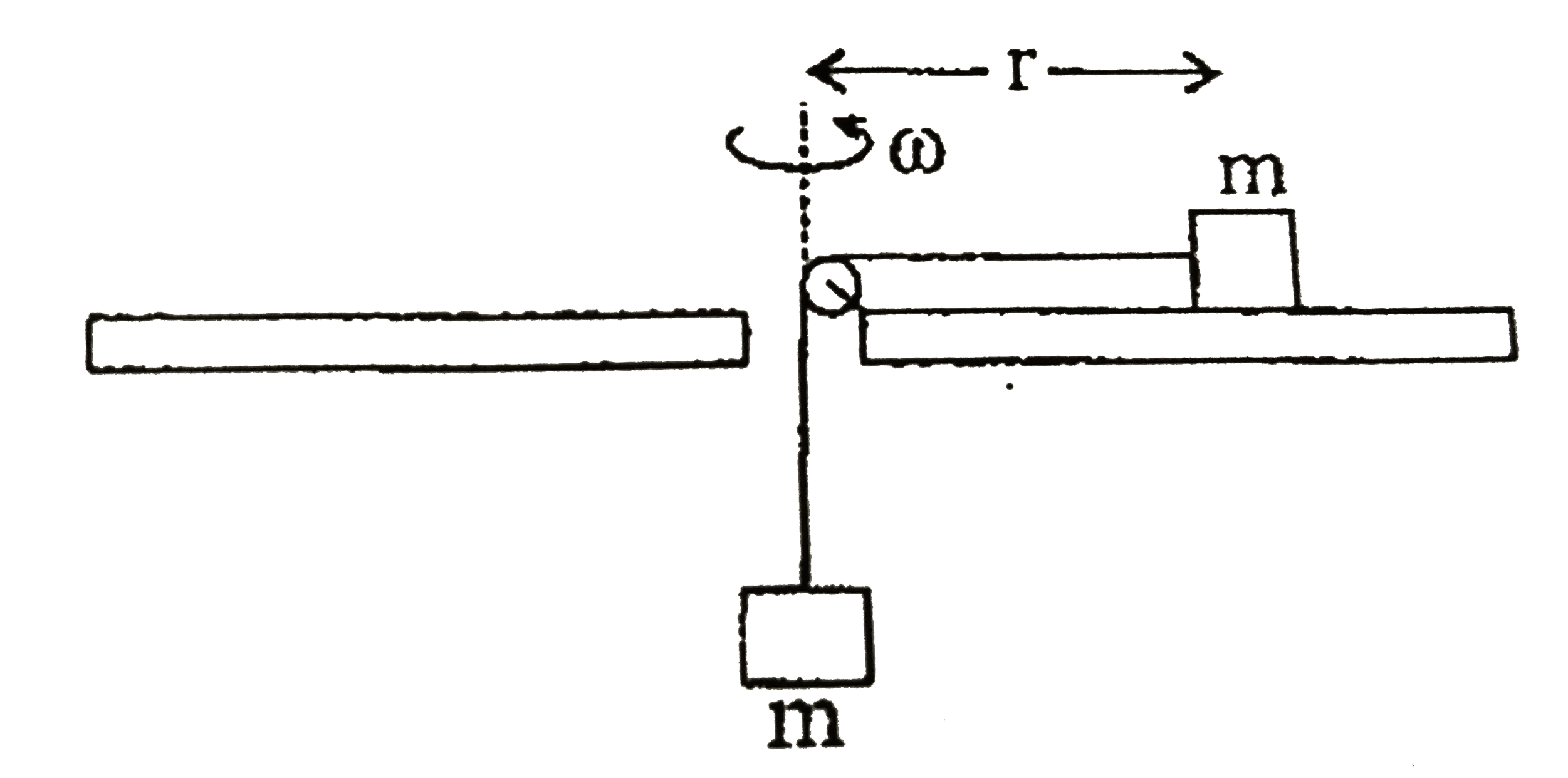
Play - Two equal masses m are attached by a string. One mass lies at radial d...
06:34
|
Playing Now - Find the velocity (in m/s) with wich a block of mass 1 kg must be hori...
06:35
|
Play - A uniform rod of length 10meters and mass 20 kilograms is balanced on ...
03:03
|
Play - Consdier the equation (d)/(dt)[intvecF.dvecs]=A[vecF.vecp] Then dime...
02:59
|
Play - A heavy particle is projected with a velocity at an acure angle with t...
04:49
|
Play - A particle is projected at an angle of 45^(@) with the horizontal with...
04:40
|
Play - Two identical rings each of mass m with their planes mutually perpendi...
06:02
|
Play - Two balls of same mass are dropped from the same height h, on to the f...
11:31
|
Play - A block of mass m is placed on a rough horizontal floor and it is pull...
06:03
|
Play - A cylist travelling at 10m/s applies brakes and stops in 25m m. The gr...
06:09
|
Play - A particle of mass m begins to slide down on a fixed smooth sphere fro...
10:23
|
Play - The velocity function of an object moving along a straight line is giv...
04:25
|
Play - A piece of paper (shown in figure-1) is in form of a square. Two corne...
05:52
|
Play - A 500 kg rocket is set of vertical firing. The relative speed of burnt...
03:32
|
Play - A mass M=40kg is fixed at the very edge oa a long plank of mass 80kg a...
09:11
|
Play - A very heavy box is kept on a frictionless incline plane inclined at a...
04:16
|
Play - Two masses m(1), and m(2) are connected by a string of length L. They ...
Text Solution
|
Play - A given object takes m times as much time to slide down a 45^(@) rough...
04:48
|
Play