Text Solution
Verified by Experts
|
Topper's Solved these Questions
TEST PAPERS
BANSAL|Exercise PHYSICS PART (A)|32 VideosView PlaylistTEST PAPERS
BANSAL|Exercise PHYSICS PART (B)|3 VideosView PlaylistTEST PAPERS
BANSAL|Exercise PHYSICS PART- C|4 VideosView PlaylistSEMICONDUCTORS
BANSAL|Exercise CBSE Question|32 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
BANSAL-TEST PAPERS-PHYSICS
- A cone of radius r and height h is kept on a turntable rotating with a...
Text Solution
|
Play - A uniform rope of length 12m and mass 12kg hangs vertically from a rig...
09:57
|
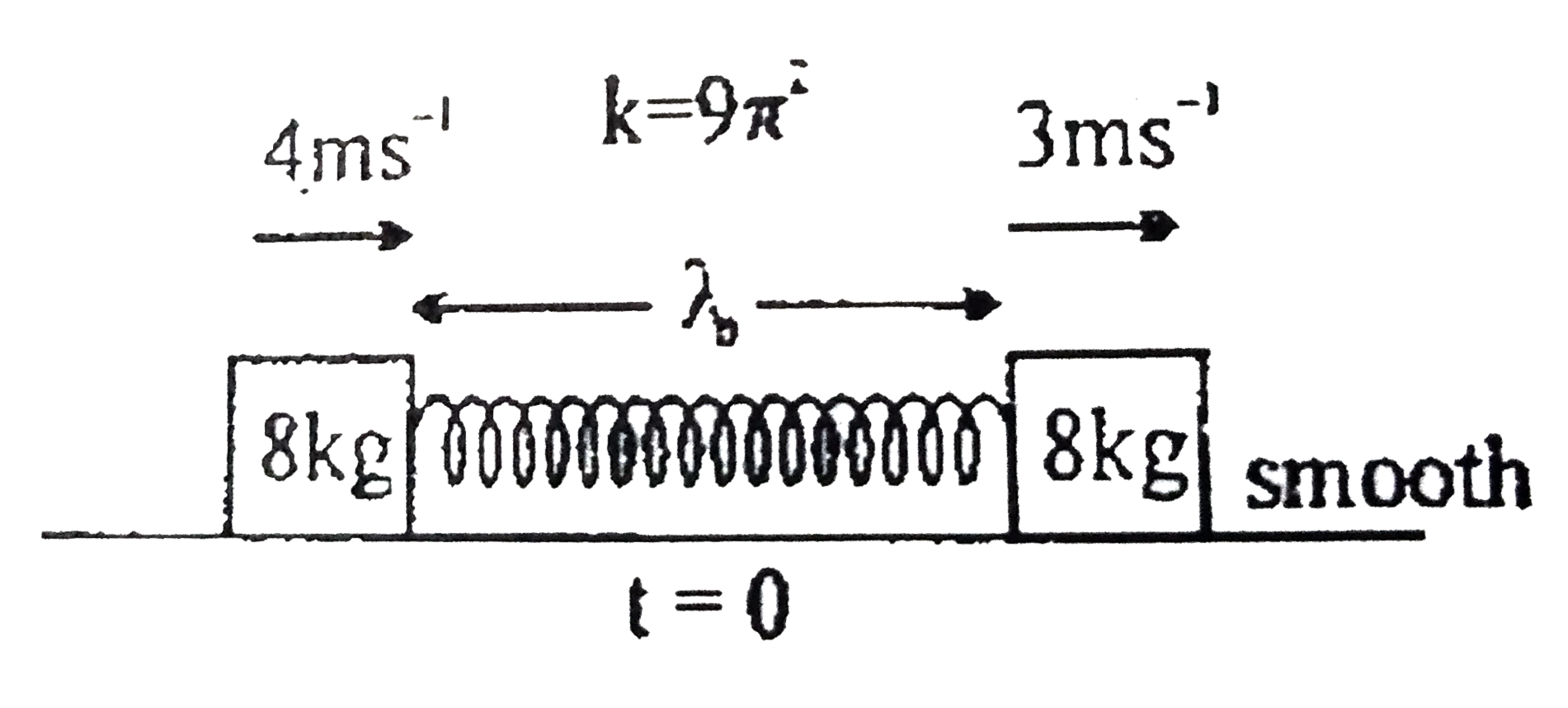
Play - Two block-spring mass system are moving on smooth horizontal surface a...
Text Solution
|
Playing Now - An elastic string has a force constant k and mass m. the string hangs ...
03:14
|
Play - A rod of mass 1kg and length 6.25 m is hinged at one end of a smooth h...
05:12
|
Play - Find longest wavelength in Lyman series of hydrogen atom spectrum.
04:37
|
Play - The de-Broglie wavelength of an electron moving in the nth Bohr orbit ...
02:14
|
Play - Calculate the half life period of a radioactive substance if its activ...
01:10
|
Play - The total energy of eletcron in the ground state of hydrogen atom is -...
01:46
|
Play - A heshly prepared radioactive source of half life 2 hrs emits radiatio...
03:52
|
Play - The average current due to an electron orbiting the proton in the n^(t...
02:21
|
Play - The radius of the shortest orbit in a one electron system is 18 pm it...
02:20
|
Play - If E1, E2 and E3 represent respectively the kinetic energies of an el...
01:40
|
Play - if the wavelength of first member of Lyman series is lambda then calcu...
04:47
|
Play - The X-ray beam coming from an X-ray tube
02:06
|
Play - A beam of ultraviolet light of all wavelength passes through hydrogen ...
03:26
|
Play - Photons are incident from vacuum on a transparent material with a refr...
02:34
|
Play - An electron collides with a fixed hydrogen atom in its ground state. H...
03:40
|
Play - Assertion : Photoelectric effect supports the quantum nature of light....
01:08
|
Play - Which of the following pails constitute very similar radiations
02:51
|
Play