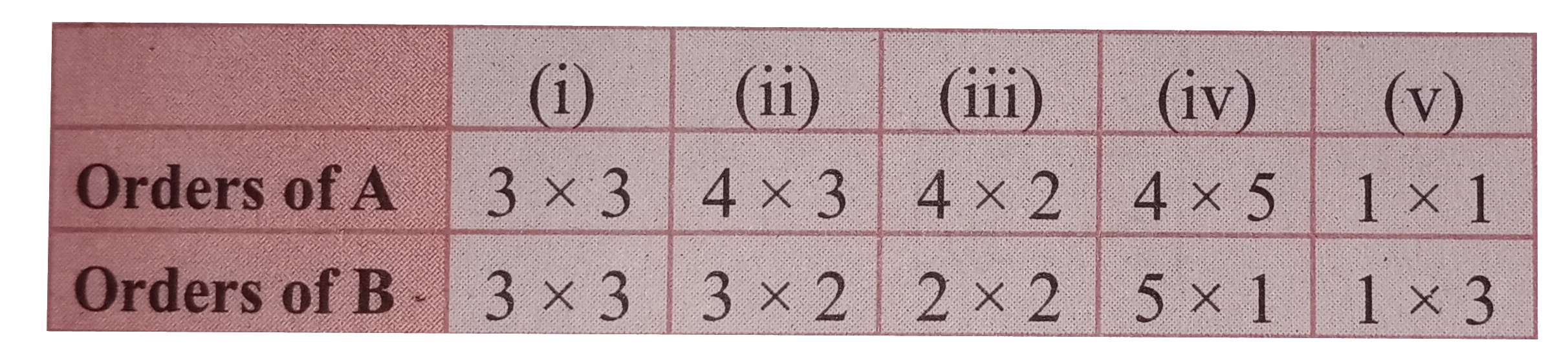Answer
Step by step text solution for Find the order of the product matrix AB is by MATHS experts to help you in doubts & scoring excellent marks in Class 10 exams.
|
Topper's Solved these Questions
ALGEBRA
FULL MARKS|Exercise Exercise 3.19|20 VideosView PlaylistALGEBRA
FULL MARKS|Exercise Unit Exercise|20 VideosView PlaylistALGEBRA
FULL MARKS|Exercise Exercise 3.17|8 VideosView PlaylistCOORDINATE GEOMETRY
FULL MARKS|Exercise ADDITIONAL QUESTIONS SOLVED (Answer the following questions)|20 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
FULL MARKS-ALGEBRA-Exercise 3.18
- Find the order of the product matrix AB is
03:33
|
Playing Now - If A is of order ptimesq and B is of order qtimesr, what is order of A...
01:43
|
Play - A has 'a' rows and 'a+3' columns. B has 'b' rows and '17-b' columns, a...
03:35
|
Play - If A=[(2, 5), (4, 3)], B=[(1, -3), (2, 5)] find AB, BA and check if AB...
03:52
|
Play - Given that A=[(1, 3), (5, -1)], B=[(1, -1, 2), (3, 5, 2)], C=[(1, 3, 2...
07:15
|
Play - Show that the matrices A=[(1, 2), (3, 1)], B=[(1, -2), (-3, 1)] satisf...
02:59
|
Play - Let A=[(1, 2), (1, 3)], B=[(4, 0), (1, 5)], C=[(2, 0), (1, 2)] show th...
04:16
|
Play - If A={:((cos theta,0),(0, cos theta)):},B={:((sin theta,0),(0, sin the...
03:13
|
Play - If A={:((cos theta,-sin theta),(sin theta, cos theta)):} prove that "A...
01:55
|
Play - Verify that A^(2) = I when A= ((5,-4),(6,-5))
03:59
|
Play - If A=((a, b), (c, d)) and I-((1, 0), (0, 1)) show that A^(2)-(a+d)A=(b...
03:58
|
Play - If A=[(5, 2, 9), (1, 2, 8)], B=[(1, 7), (1, 2), (5, -1)] verify that (...
04:54
|
Play - If A={:((3,1),(-1,2)):} show that A^(2)-5A+7I(2)=0
03:07
|
Play