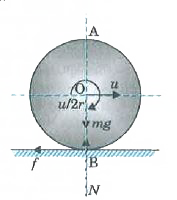
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
MODERN PUBLICATION|Exercise COMPETITION FILE (OBJECTIVE TYPE QUESTIONS (ASSERTION REASON TYPE QUESTIONS) )|10 VideosView PlaylistSYSTEMS OF PARTICLES AND ROTATIONAL MOTION
MODERN PUBLICATION|Exercise COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS (MATCHING TYPE QUESTIONS) )|3 VideosView PlaylistSYSTEMS OF PARTICLES AND ROTATIONAL MOTION
MODERN PUBLICATION|Exercise COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS (JEE (Main) & Other State Boards for Engineering Entrance) )|48 VideosView PlaylistPHYSICAL WORLD
MODERN PUBLICATION|Exercise Revision exercises (Long answer questions)|6 VideosView PlaylistTHERMAL PROPERTIES OF MATTER
MODERN PUBLICATION|Exercise CHAPTER PRACTICE TEST|15 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
MODERN PUBLICATION-SYSTEMS OF PARTICLES AND ROTATIONAL MOTION-COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS MULTIPLE CHOICE QUESTIONS (with more than one correct answer) )
- A sphere and a block both are released from rest at the top of an incl...
Text Solution
|
Play - Consider a body of mass 1.0 at rest at the origin at time t = 0. A ...
03:33
|
Play - State of the sphere at some instant of time is shown in figure. Surfac...
Text Solution
|
Playing Now - A ring performs pure rolling on a horizontal surface and its state at ...
Text Solution
|
Play - Two solid spheres P and Q are released from rest from the same point o...
07:44
|
Play - A solid cylinder is rolling down the inclined plane without slipping. ...
05:18
|
Play - The position vector vec(r) of a particle of mass m is given by the fo...
07:40
|
Play - Two thin circular discs of mass m and 4m, having radii of a and 2a, re...
11:36
|
Play - A block of mass M has a circular cut with a frictionless surface as sh...
07:50
|
Play - Sphere of mass M and radius R is kept on a rough horizontal floor. A s...
03:40
|
Play - Sphere of mass M and radius R is kept on a rough horizontal floor. A s...
Text Solution
|
Play - Sphere of mass M and radius R is kept on a rough horizontal floor. A s...
Text Solution
|
Play - Small sphere of mass m and radius r is kept on fixed inclined rough su...
05:32
|
Play - Small sphere of mass m and radius r is kept on fixed inclined rough su...
08:30
|
Play - Small sphere of mass m and radius r is kept on fixed inclined rough su...
02:50
|
Play - State of motion of the sphere at t = 0 is described in figure, Centre ...
07:32
|
Play - State of motion of the sphere at t = 0 is described in figure, Centre ...
Text Solution
|
Play - State of motion of the sphere at t = 0 is described in figure, Centre ...
Text Solution
|
Play - A frame of reference that is accelerated with respect to an inertial f...
20:36
|
Play - A frame of reference that is accelerated with respect to an inertial f...
20:36
|
Play