Text Solution
Verified by Experts
|
Topper's Solved these Questions
ELECTROSTATICS
MBD -HARYANA BOARD|Exercise OBJECTIVE TYPE QUESTIONS|23 VideosView PlaylistELECTROSTATICS
MBD -HARYANA BOARD|Exercise SHORT ANSWER TYPE QUESTIONS|11 VideosView PlaylistElectromagnetic Waves
MBD -HARYANA BOARD|Exercise Example|7 VideosView PlaylistMAGNETISM
MBD -HARYANA BOARD|Exercise OBJECTIVE TYPE QUESTIONS|17 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
MBD -HARYANA BOARD-ELECTROSTATICS-LONG ANSWER TYPE QUESTIONS
- State Coulomb's law of force in electrostatics. Express it in vector f...
02:33
|
Play - What is an electric dipole? Derive expression of electric field intens...
Text Solution
|
Play - Derive a relation for electric field of an electric dipole at a point ...
08:27
|
Play - State and prove Gauss's law in electrostatics.
05:01
|
Play - A charge is distributed uniformly over a ring of radius ‘a’. Obtain an...
11:53
|
Play - Define capacitance of a parallel plate capacitor,Derive an expression ...
06:40
|
Play - Derive expresion for capacitance of a parallel plate capacitor and exp...
Text Solution
|
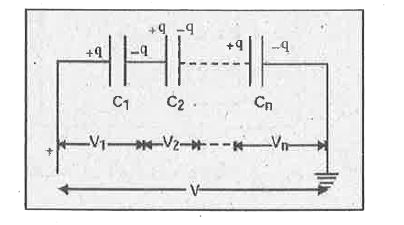
Playing Now - Find the final charge on each capacitor if they are connected as shown...
06:25
|
Play - Derive an expression for the capacitance of a parallel plate capacitor...
Text Solution
|
Play - Write different expression for the energy stored in a capacitor.
01:27
|
Play - Determine electric field intensity near an infinitely long straight un...
Text Solution
|
Play - Derive an expression for electric intensity E due to a uniformly charg...
04:34
|
Play - Electric field intensity at a point due to an infinite sheet of charge...
01:47
|
Play - Two identical resistors, each of resistance 15ohm are connected in (i)...
03:46
|
Play