Text Solution
Verified by Experts
|
Topper's Solved these Questions
ELECTROMAGNETIC INDUCTION
NEW JOYTHI PUBLICATION|Exercise SOLUTIONS TO EXERCISES FROM NCERT TEXT|14 VideosView PlaylistELECTROMAGNETIC INDUCTION
NEW JOYTHI PUBLICATION|Exercise PRACTICE PROBLEMS FOR SELF ASSESSMENT|3 VideosView PlaylistELECTRIC CHARGES AND FIELDS
NEW JOYTHI PUBLICATION|Exercise Competitive Exam Corner|20 VideosView PlaylistELECTROMAGNETIC WAVES
NEW JOYTHI PUBLICATION|Exercise COMPETITIVE EXAM CORNER|16 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
NEW JOYTHI PUBLICATION-ELECTROMAGNETIC INDUCTION -COMPETITIVE EXAM CORNER
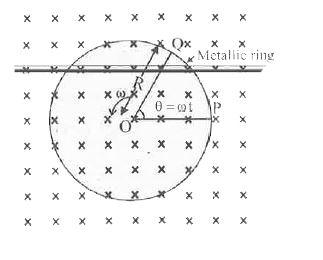
- A metallic rod of 1m length is rotated with a frequency of 50 rev/s, w...
04:04
|
Playing Now - A 50 Hz ac current of peak value 2 A flows through one of the pair of ...
03:24
|
Play - The unit of self-inductance is
01:34
|
Play - A 0.1 m long conductor carrying a current of 50 A is held perpendicula...
03:14
|
Play - Two solenoids of equal number of turn have their lengths and the radii...
02:48
|
Play - Two identical coaxial coils P and Q carrying equal amount of current i...
02:41
|
Play - The self inductance of a long solenoid cannot be increased by
01:42
|
Play - The rate of change of current of 10As^(-1) in a coil produces an emf o...
01:17
|
Play - The magnetic flux (in weber) linked with a coil of resistance 10Omega ...
02:16
|
Play - The self-inductance of an air core solenoid of 100 turns is 1 mH. The ...
04:02
|
Play - Identify the wrong statement
03:52
|
Play - Electromagnetic induction is not used in
02:10
|
Play - The polarity of induced emf is given by
02:06
|
Play - A conducting ring of radius 1 m kept in a uniform magnetic field B of ...
02:58
|
Play