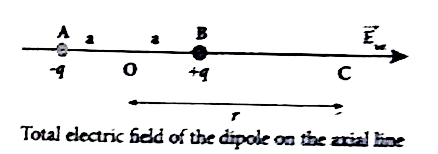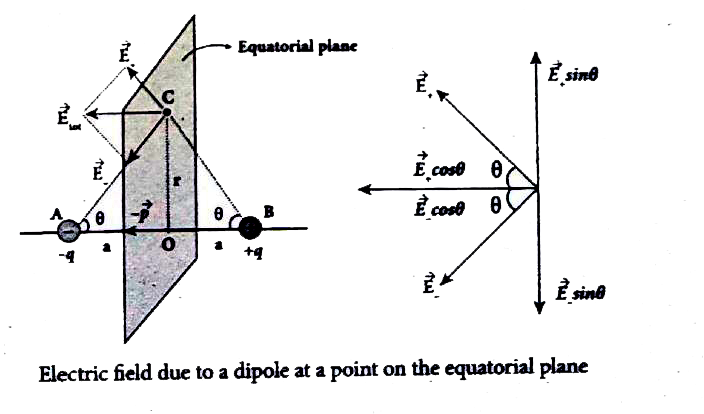Electric field due to an electric dipole at points on the axial line. Consider an electric dipole placed on the x-ax is as shown in figure. A point C is located at a distance of r from the midpoint O of the dipole along the axial line,.

`vecE=1/(4piepsilon_0)q/((r-a)^2)` along BC
since the electric dipole moment vector `vecp` is from -q to +q and is directed along BC, the above equation is rewritten as
`vecE_(+)=1/(4pivarepsilon_0)q/((r-a)^2)hatp` ........(1)
`vecE=1/(4pivarepsilon_0)q/((r-a)^2)hatp` ...........(2)
where `hatp` is located closer to the point C than `-q,vecE_(-).vecE_(+)` us stronger than `vecE_(-)` . therefore the length of the `vecE_(+)` vector is drawn large than that of `vecE_(-)` vector.
The total electric field at point C is calculated using the superposition of the electric field
`vecE_("tot")=vecE_(+)+ vecE_(-)` .............(3)
`=1/(4pivarepsilon_0)q/((r-a)^2)hatp-1/(4pivarepsilon_0)q/((r-a)^2)hatp rArr vecE_("tot")=1/(4pivarepsilon_0)(1/((r-a)^2)-1/((r+a)^2))hatp` ............(4)
`vecE_("tot")=1/(4pivarepsilon_0)q((4ra)/((r^2-a^2)^2))hatp` ..............(5)
Note that total electric field is along `vecE_(+)` since +q is closer to C than -q.
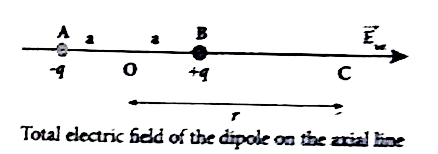
The direction of `vecE_("tot")` is shown in figure
If the point C is very far away from the dipole then `(r gt gt a)` .
Under this limit the term `(r^2-a^2)^2~~r^4` Substituting this into equation we get
`vecE_("tot")=1/(4pivarepsilon_0)((4aq)/(r^3))hatp(r gt gt a)`
since 2aq `hatp=vecp`
`vecE_("tot")1/(4pivarepsilon_0)(2vecp)/(r^3) (r gt gt a)`
If the C is chosen on the left side of the dipole the total electric field is still in the direction of `vecp` .
Case (ii) Electric field due to an electric dipole at a point on the equatorial plane
Consider a point C at a distance r from the midpoint O of the dipole on the equatorial plane as shown in figure. since the point C is equi-distance from +q and -q , the magnitude of the electric field of +q and -q are the same. The direction of `vecE_(+)` is along BC and the direction of `vecE_(-)` is along CA.
`vecE_(+) and vecE_(-)` are resolved into two components one component parallel to the dipole axis and the other perpendicular to it . The perpendicular components `|vecE_(-)| sin theta and |vecE_(-)| sin theta` are oppositely directed and cancel each other. The magnitude of the total electric field at point C is
the sum of the parallel components of `vecE_(+) and vecE_(-)` and its direction is along `-hatp`.
`vecE_("tot")=-|vecE_(+)| cos theta hatp-|vecE_(-)| cos theta hatp` ........(1)
The magnitude `vecE_(+) and vecE_(-)` are the same and are given by
`|vecE_(+)|=|vecE_(-)|=1/(4pivarepsilon_0)q/((r^2+a^2))` ..............(2)
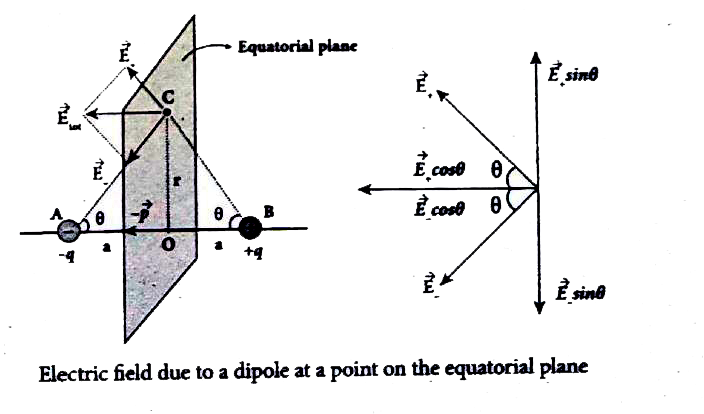
By substituting equation (1) into equation (2) ,we get
`vecE_("tot")=-1/(4pivarepsilon_0)(2q cos theta)/((r^2+a^2))hatp=-1/(4pivarepsilon_0)(2qa)/((r^2+a^2)^(3/2))hatp` sinc `cos theta =a/sqrt(r^2+a^2)`
`vecE_("tot")=-1/(4pivarepsilon_0)(vecp)/((r^2+a^2)^(3/2))` since `vecp=2qa hatp` ............(3)
At very large distance `(r gt gt a)` the equation becomes
`vecE_("tot")=-1/(4pivarepsilon_0)p/(r^3) (r gt gt a)` ............(4)