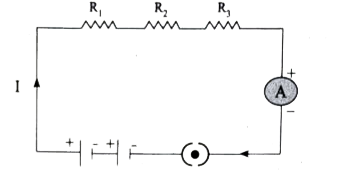
Let, three resistances `R_(1), R_(2)" and "R_(3)` be connected in series. Let the current flowing through them be I. According to Ohm.s Law, the potential differences `V_(1), V_(2)" and "V_(3)" across "R_(1), R_(2)" and "R_(3)` respectively, are given by:
`V_(1)=IR_(1) " ......(1)"`
`V_(2)=IR_(2)" ......(2)"`
`V_(3)=IR_(3)" ......(3)"`
The sum of the potential differences across the ends of each resistor is given by
`V=V_(1)+V_(2)+V_(3)`
Using equation (1), (2) and (3), we get
`V=IR_(1)+IR_(2)+IR_(3)" ......(4)"`
The effective resistor is a single resistor, which can replace the resistors effectively, so as to allow the same current through the electric circuit. Let, the effective resistance of the series-combination of the resistors, be `R_(s)`.
Then,
`V=IR_(s)" ...... (5)"`
Combining equations (4) and (5) we get,
`IR_(s)=IR_(1)+IR_(2)+IR_(3)`
`R_(s)=R_(1)+R_(2)+R_(3)" ...... (6)"`
Thus, When a number of resistors are connected in series, their effective resistance is equal to the sum of the individual resistances.
When .n. resistors of equal resistance R are connected in series, the equivalent resistance is .n R. .i.e., `R_(s)=nR`
The equivalent resistance in a series combination is greater than the highest of the individual resistances.
