According to Ohm.s law, at a constant temperature, the steady current .I. flowing through a conductor is directly proportional to the potential difference .V. between the two ends of the conductor.
1`propV. :. V=1R`
(a)(ii)Resistors in Parallel: A parallel circuit has two or more loops through which current can pass. If the circuit is disconnected in one of the loops, the current can still pass through the other loop(s). The wiring in a house consists of parallel circuits.
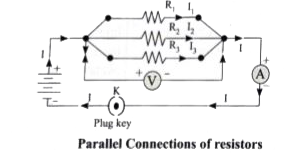
(i) Consider that three resistors `R_1 R_2` and `R_3` are connected across two common points A and B.
(ii) The potential difference across each resistance is the same and equal to the potential difference between A and B. This is measured using the voltmeter.
(iii) The current I arriving at A divides into three branches `I_1,I_2`, and `I_3`, passing through `R_1 R_2` and `R_3` respectively.
According to the Ohm’s law we have
`I_(1)=(V)/(R_1)` ……(1)
`I_2=(V)/(R_2)`...(2)
`I_3=(V)/(R_3)`...(3) The total current through the circuit is given by `I=I_1+I_2+I_3`
Using equation (1),(2) and (3) we get
`I=(V)(R_1)+(V)(R_2)+(V)(R_3)`......(4)
Let the effective resistance of the parallel combination of resistors be `R_p`. Then, `I=(V)/(R_(p))`...(5)
`(V)/(R_(p))=(V)(R_1)+(V)(R_2)+(V)(R_3)`
`(1)/(R_(p))=(1)(R_1)+(1)(R_2)+(1)(R_3)`
Thus
(iv)When a number of resistor are connected in parallel the sum of the reciprocals of the individual resistance is equal to the reciprocal of the effective or equivalent resistance.
(v)When ‘n’ resistor of equal resistance R are connected in parallel the equivalent resistance is `(R)/(n)`
i.e `(1)/(R_(p))=(1)(R)+(1)(R)+(1)(R)`........+`(1)/(R)=n/R`
Hence `R_(p)=(R)/(n)`
(vi) The equivalent resistance in a parallel combination is less than the lowest of the indiviuasal resistances.
