Junction. It is apont where two or more conductors are connected to source and current gets distributed at the point.
Loop. Loop is a closed path of an electric circuit.
Kirchhoff.s First Law of Junction Rule.
It states that the algebraic sum of currents meeting at a point is zero.
This law is also called Kirchhoff.s current law.
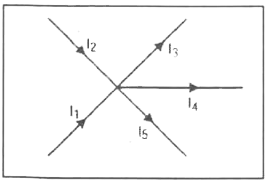
To explain this law, consider a number of wires connected at a point P. currents `i_(1),i_(2),i_(3),i_(4)` and `i_(5)` flow through these wires in the directions as shown in the figure.
Sign conventions
(i) The currents approaching the point P be taken as positive.
(ii) Current flowing away from it be taken as negative.
According to Kirchhoff.s first law,
`i_(1)+i_(2)-i_(3)-i_(4)-i_(5)=0`
or `sumi=0`
The most evident conclusion of this law is that the current entering a point must be the same as that leaving. hence there cannot be any accumulation for current at any point in a conductor.
Kirchhoff.s Second Law or Loop Rule
It states that in a closed electric circuit, the algebraic sum of e.m.f.s is equal to the algebraic sum of the product of the resistances and the currents flowing through them. this law may be called Kirchhoff.s voltage Law.
Sign Convenstions
Select any point on the loop and traverse the loop once in any direction clockwise or anticlockwise.
(i) If the direction of flow of current in a resistance is the same as that of traversing the loop, the product of the resistance and the current flowing through it is taken as positive and vice-versa.
(ii) While traversing the loop, if -ve pole of a cell is encountered first then its e.m.f. is taken as +ve, otherwise negative.
The resistance of a conductor has no sign. the sign of the product of the current the resistance will, therefore, be decided by the sign of electric current.
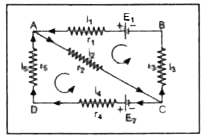
Considering circuit ABCA, we have
`E_(1)=i_(1)r_(1)+i_(2)r_(2)+i_(3)r_(3)`
In circuit ABCDA, we have
`E_(1)-E_(2)=i_(1)r_(1)-i_(5)r_(5)-i_(4)r_(4)+i_(3)r_(3)`
Conditions of balanced wheatstone bridge
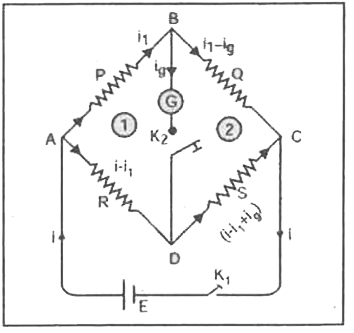
Wheatstone bridge consists of four resistors, P,Q,R and S, the last one is unknown.
The distribution of the current is as shown in the figure.
Applying Kirchhoff.s law to circuit 1 i.e., ABDA, we have
`0=i_(1)P+i_(g)G-(i-i_(1))R`
When bridge is balanced `i_(g)=0`
`therefore 0=i_(1)P(i-i_(1))R`
When bridge is balanced, `i_(g)=0`
`therefore 0=i_(1)P(i-i_(1))R`
or `i_(1)P=(i-i_(1))R` . . . (i)
Applying Kirchhoff.s law to second circuit i.e., BCDB, we have
`0=(i_(1)-i_(g))Q-(i-i_(1)+i_(g))S-i_(g)G`
For balanced bridge, `i_(g)=0`
`therefore 0=i_(1)Q-(i-i_(1))S`
or `i_(1)Q=(i-i_(1))S` . . (ii)
Dividing (i) by (ii), we have
`(i_(1)P)/(i_(1)Q)=((i-i_(1))R)/((i-i_(1))S)`
`P/Q=R/S`
This is the principle of Wheatstone.s bridge.


