A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
OSCILLATIONS
MODERN PUBLICATION|Exercise Competition File (JEE (Advanced) For IIT Entrance)|7 VideosView PlaylistOSCILLATIONS
MODERN PUBLICATION|Exercise Competition File (Multiple choice question)|11 VideosView PlaylistOSCILLATIONS
MODERN PUBLICATION|Exercise Competition File (Multiple choice questions) AIPMT/NEET other State Boards for Medical Entrance|14 VideosView PlaylistMOTION IN A STRAIGHT LINE
MODERN PUBLICATION|Exercise CHAPTER PRACTICE TEST|16 VideosView PlaylistPHYSICAL WORLD
MODERN PUBLICATION|Exercise Revision exercises (Long answer questions)|6 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
MODERN PUBLICATION-OSCILLATIONS -Competition file (Multiple choice question) JEE (Main) & Other State Boards for Engineering Entrance
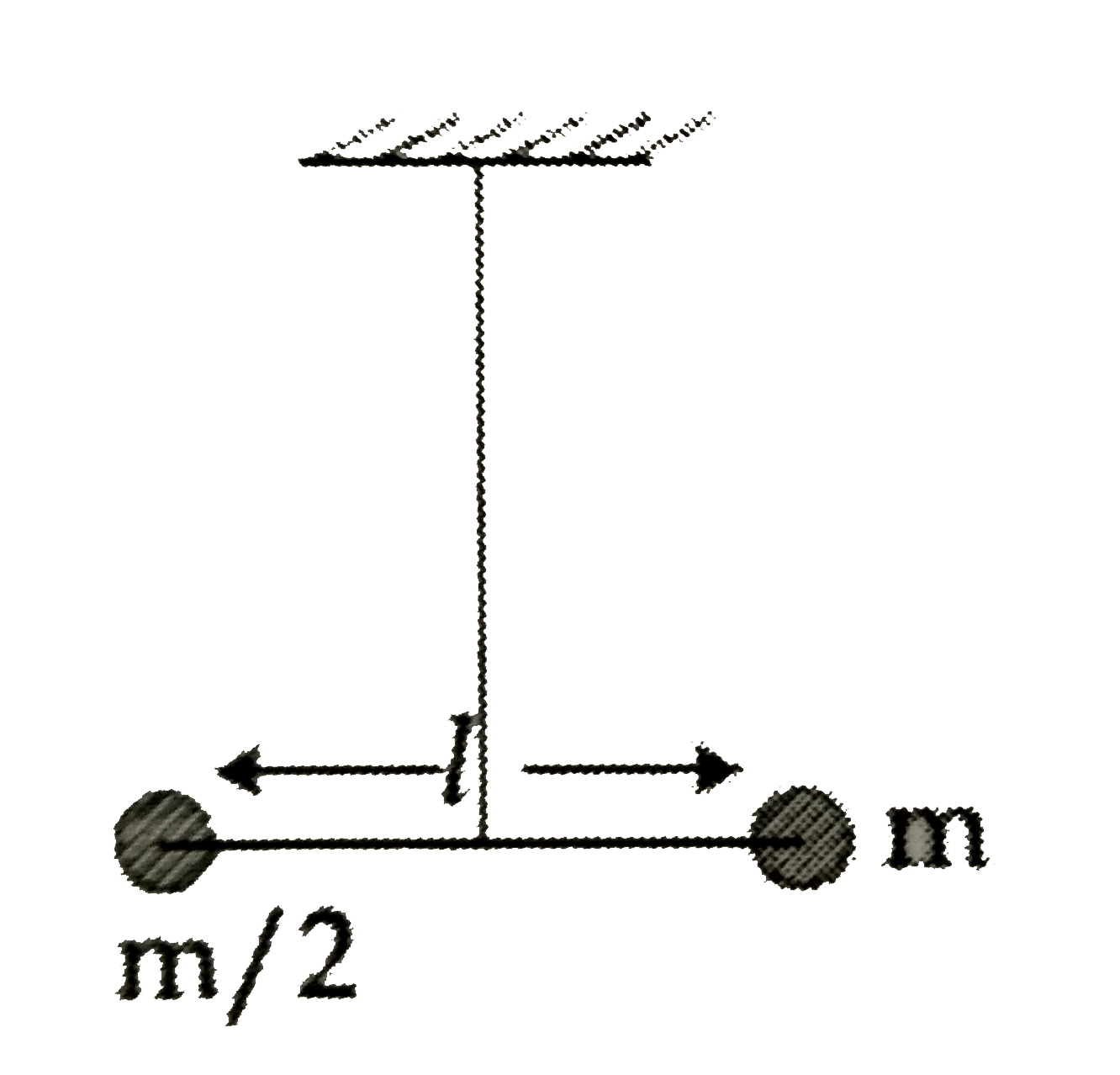
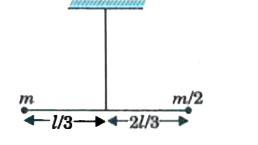
- Two masses m and (m)/(2) are connected at the two ends of a massless r...
07:10
|
Playing Now - A particle executes simple harmonic motion and is located at x = a, b...
06:01
|
Play - A point mass oscillates along the x-axis according to the law x=x(0) c...
03:25
|
Play - A rod of mass 'M' and length '2L' is suspended at its middle by a wire...
08:10
|
Play - Two particles are executing simple harmonic of the same amplitude (A) ...
05:59
|
Play - A massless spring (k = 800 N/m), attached with a mass (500 g) is compl...
06:59
|
Play - A wooden cube (density of wood 'd') of side 'l' flotes in a liquid of ...
01:39
|
Play - A particle of mass m is at rest at the origin at time t=0 It is subjec...
03:17
|
Play - If a simple pendulum has significant amplitude (up to a factor of1//e ...
03:12
|
Play - The displacement of a damped harmonic oscillator is given by x(t)=e^(-...
04:47
|
Play - An ideal gas enclosed in a cylindrical container supports a freely mov...
05:53
|
Play - A particle moves with simple harmonic motion in a straight line. In fi...
08:24
|
Play - For a simple pendulum, a graph is plotted its kinetic energy (KE) and ...
02:59
|
Play - A particle performs simple harmonic mition with amplitude A. Its speed...
05:21
|
Play - If x, v and a denote the displacement, the velocity and the accelerati...
04:23
|
Play - A pendulum with time period of 1s is losing energy due to damping. At ...
03:35
|
Play - Two particles are executing SHM in a straight line. Amplitude A and th...
03:53
|
Play - A 1 kg block attached to a spring vibrates with a frequency of 1 Hz on...
01:57
|
Play - The ratio of maximum acceleration to maximum velocity in a simple harm...
02:33
|
Play - If an experiment to determine the period of a simple pendulum of lengt...
06:44
|
Play